Perpendicular Bisectors, Angle Bisectors, and Circumcenters
Follow these steps to construct perpendicular bisectors
1) Using the COMPASS TOOL, create a circle with radius AB and center point A
2) Using the COMPASS TOOL, create a circle with radius AB and center point B
3) Using the SEGMENT TOOL, draw a segment that connects the intersections of circles A and B
4) Using the POINT TOOL, mark point E at the intersection of segments AB and CD
RESULTS: Segment CD is the Perpendicular Bisector of segment AB
Point E is the Midpoint of segment AB
Construction #1
Check Your Understanding
What does the term perpendicular bisector mean?
Follow these steps to bisect an angle:
1) Using the POINT TOOL, mark point D on segment AB
2) Using the COMPASS TOOL, create a circle with radius AD and center point A
3) Using the POINT TOOL, mark point F where circle A intersects segment AC
4) Using the COMPASS TOOL, create a circle with the radius DF and center point D
5) Using the COMPASS TOOL, create a circle with the radius DF and center point F
6) Using the SEGMENT TOOL, draw a segment from point A to the intersection of circles D and F
RESULTS: Segment AG is the Angle Bisector of angle CAB
Check Your Understanding
What does the term angle bisector mean?
The Circumcenter of a Triangle
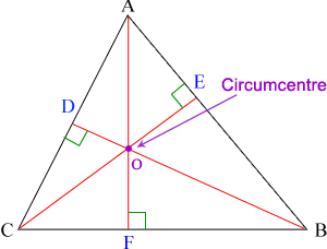
![[color=#222222][size=100][size=150]The circumcenter of a triangle can be in different places based on the type of triangle. [/size][/size][/color]](https://www.geogebra.org/resource/khkmpvkq/npben1LLgUqqlkzm/material-khkmpvkq.png)
Check Your Understanding
The circumcenter is the intersection of which 3 lines in a triangle?
Think About It
If you needed to find the balancing point of a triangle, what would you do? Which steps would you take to find the balancing point (center of gravity)?