In un triangolo con lati disuguali angoli opposti disuguali
- Autore:
- Gian Lodovico Miari
Vogliamo dimostrare che In un triangolo con due lati disuguali, anche gli angoli opposti sono disuguali ed a lato maggiore sta opposto angolo maggiore.
Prova a seguire le indicazioni per la costruzione in Geogebra utilizzando il programma scaricato oppure il foglio qui sotto:
- Apri un nuovo foglio, chiudi la vista algebra, nascondi gli assi cartesiani e attiva la griglia nella finestra grafica
Disegna i vertici di un triangolo a piacere ABC con la condizione che almeno due lati siano disuguali, ad esempio AB>AC
Con lo strumento segmento congiungi i punti e ottieni la poligonale chiusa contorno del nostro triangolo.
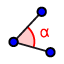Con lo strumento angolo puoi misurare gli angoli al vertice del triangolo
Dalle misure risulta vero l'enunciato? 
Spostando ad esempio C, la relazione continua ad essere vera.
- Passiamo ora alla dimostrazione
- Individuiamo sul lato AB un punto D tale che AD=AC. Con riga e compasso punteremmo il compasso in A con apertura _____ e _____. In Geogebra
utilizziamo lo strumento compasso (indicando il centro A e apertura/raggio AC) e poi individuiamo D come 
punto di intersezione tra _____________ e __________ - Congiungiamo C con D.
Il triangolo ADC risulta isoscele e quindi gli angoli alla base
Se consideriamo il triangolo BCD, l'angolo ADC è
Per il teorema dell'angolo esterno: ACB>ACD. Il teorema afferma
Infine osserviamo che ACB>ACD
Rileggiamo le relazioni trovate:
ACB>ACD
ACD=ADC
ADC>ABC
Possiamo concludere che ACB>ABC. E il teorema è dimostrato
Se hai trovato difficoltà a costruire il disegno con Geogebra guarda questo foglio (puoi seguire la costruzione con i pulsanti in basso)