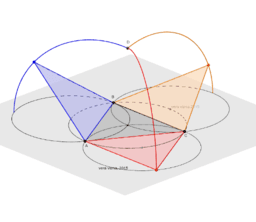
Nesta construção, o trIângulo equilátero [ABC] pertencente a um plano horizontal, é uma das faces de um tetraedro regular.
Os seguintes pontos podem ser livremente movimentados:
- o ponto A, para alterar a dimensão da aresta do tetraedro;
- o ponto azul, ao longo do arco de circunferência azul (que resulta da intersecção das esferas de centro em A e em B e raio igual a [AB]);
- o ponto laranja, ao longo do arco de circunferência laranja (que resulta da intersecção das esferas de centro em B e em C e raio igual a [BC]);
- o ponto vermelho, ao longo do arco de circunferência da mesma cor (que, por sua vez, resulta da intersecção das esferas de centro em A e em C e raio igual a [AC]);
Um tetraedro regular é obtido quando cada um destes pontos coincide com o vértice D (que resulta da intersecção das três esferas).
Para não confundir a construção:
- as esferas referidas não foram representadas;
- foi determinada apenas a intersecção das três esferas localizada acima do plano horizontal.
A vista gráfica pode ser livremente rodada para melhor compreensão do que se pretende explicar, dado que se trata de uma representação em ambiente tridimensional virtual.
