Quadrilaterals with one pair of equal opposite sides and one pair of equal opposite angles definitely share some properties with parallelograms, but are they actually parallelograms? Or more importantly, what are the conditions that guarantee a parallelogram?
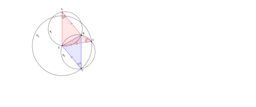
The picture here shows two identical circles K_1 and K_2. With BD as a common chord, the angles subtended in the segments will be equal, therefore angle BAD equals angle BCD (and angle BC'D). Circle K_3 is centered at D with radius equal to AB.
As you drag the point A, what do you notice? When are the quadrilaterals actually parallelograms?