Kalon mosque - spandrel of the east iwan - gp
Kalon mosque (12th century, rebuilt early 16th century)
The Kalon mosque of Bukhara is one of the largest mosques in Central-Asia. It is opposed to the Mir-i-Arab Madrassa, forming together the Po-i-Kaylon complex.
Detailed information you can find at orientalarchitecture.com.
The mosque is built as Friday mosque with a capacity of 12 000 people to gather the whole male population of Bukhara.
east Iwan
The geometrical decoration of the iwan combines 12- and 9-pointed stars. In the applet below you can see that these are generated by a tiling of dodecagons, enneagons and hexagonal ties.
Figure 1 illustrates that indeed with regular dodecagons, enneagons and ties one can crceate a tiling.
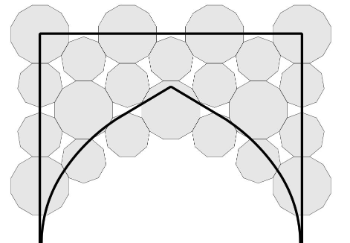
The classic way in constructing is combining the mids of the edges of the polygons.
- 12-4 star: - mark the middle of an edge of a dodecagon, - count 4 edges further on and mark the middle of it, - connect both points, - repeat these steps for all edges, - draw a 12-pointed star.
- 9-3 star: now count 3 edges further and construct a 9-pointed star.
a kite in the ties
Adding the ties creates a larger dodecagon around the dodecagon.
But this line pattern doesn't match the real pattern.
Look at figure 2: Drawing a line from a point of the star, it doesn't run through another point of the star, in other words: in the real patterns the middles of edges aren't connected to one another. Why not?
The reason is simple: the drawn pattern needs a kink to result in a kink within the tie which is not likeable.

adapting a 12-4 star
The applet below shows a 12-4 star.
Drag the green point. Now the middles of the edges are connectes with points somewhere between the middle and a vertex of the dodecagon.
While dragging you notice that the angles of the star widen. The result for the pattern is a waving instead of a straight line and the creation of kites in the ties.
The right pattern
To obtain kites within the ties we must reverse the logic.
Don't start with the lines in the dodecagon but with those in the enneagon.
- Define the middles of adjacent edges of a dodecagon and two enneagons.
- Construct in both enneagons a line that belongs to a 9-3 star.
- Draw the lines through the middle of the edge of the dodecagon and the middles on the enneagons and define for both lines the intersection with the corresponding 4th edge in the dodecagon.
- This defines the top angle of the 12-ppointed star. Now you can construct a 9-3 star in the enneagons and in the dodecagon a star, so that lines create a kite within the ties.