Le equazioni
Vogliamo scrivere le equazioni generali che descrivono la trasformazione del punto P nel suo simmetrico rispetto all'asse ax+by+c=0.
Un caso semplice
Prima di affrontare il caso generale vediamo un caso semplice, ovvero il caso in cui l'equazione generica dell'asse è x=k (ovvero siamo nel caso in cui b=0).
Osserviamo che questo è un caso che si trova molto spesso nella vita di tutti i giorni, come puoi vedere nell'immagine qui sotto:
Dato un punto P, l'equazione della trasformazione la otteniamo imponendo che:
- Il punto medio M tra P e P' appartenga alla retta x=k
- La retta PP' sia perpendicolare alla retta x=k
Prova Tu!
Il punto P', simmetrico di P=(1,2) rispetto all'asse x=3, ha coordinate:
Caso generale
Visto che il caso b=0 lo abbiamo trattato a parte, possiamo considerare la scrittura seguente della retta:
dove e
Siano quindi l'equazione della retta r, il punto iniziale e P' il simmetrico di P rispetto all'asse r.Le equazioni della trasformazione le otteniamo imponendo le due condizioni che definiscono la simmetria assiale, ovvero:
- il punto medio M appartiene alla retta r
- la retta PP' deve essere perpendicolare ad r quindi il suo coefficiente angolare m' deve essere
Prova Tu!
Guarda attentamente l'immagine qui sotto:
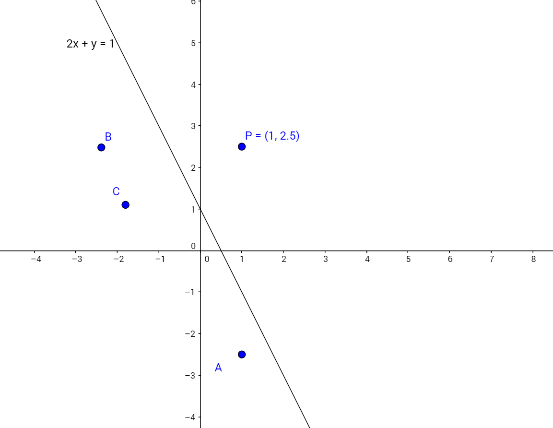
Il punto simmetrico di P=(1,2.5) rispetto all'asse 2x+y=1 é:
Nieuw didactisch materiaal
- Segno dei coefficienti di una parabola - Pratica
- Costruzione della perpendicolare a una retta passante per un suo punto
- Teorema di Cramer per sistemi 2x2 e 3x3
- Vettori: moltiplicazione di un vettore per uno scalare
- Circonferenza goniometrica interattiva - Valori esatti delle funzioni goniometriche di angoli notevoli