Otros procedimientos para construir figuras
Hay otras herramientas para construir figuras. Son las siguientes:
- "Pirámide"
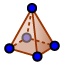 , a partir del polígono de la base y del vértice de la figura.
, a partir del polígono de la base y del vértice de la figura. - "Prisma"
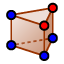 , a partir del polígono de la base y un punto de la base superior.
, a partir del polígono de la base y un punto de la base superior. - "Cono"
 , a partir del centro de la base, el vértice y introduciendo el radio de la circunferencia de la base.
, a partir del centro de la base, el vértice y introduciendo el radio de la circunferencia de la base. - "Cilindro"
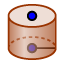 , a partir de los centros de las dos bases, la inferior y la superior, y introduciendo el radio de de las circunferencias.
, a partir de los centros de las dos bases, la inferior y la superior, y introduciendo el radio de de las circunferencias.
Recta perpendicular a un plano
Con las herramientas anteriores necesitamos siempre un punto que no esté en el plano de la base. Siempre podemos dibujarlo en dicho plano y luego "subirlo" o "bajarlo" con el ratón pero, a menudo, será necesario que se halle sobre una recta determinada perpendicular al plano. Para ello, haremos lo siguiente:
- Dibujad un punto en el plano de la base.
- Clicad en la herramienta "Recta perpendicular"
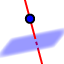 y seleccionad el punto y, seguidamente, el plano de la base.
y seleccionad el punto y, seguidamente, el plano de la base. - Dibujad un punto sobre dicha recta con las herramientas
 o
o  clicando sobre la recta.
clicando sobre la recta. - Probad de mover los dos puntos.
Trabajemos con las herramientas agrupadas
Vamos a practicar con el conjunto de herramientas que hemos enumerado para la construcción de de prismas, pirámides, conos y cilindros. También hemos agrupado las herramientas para medir longitudes y calcular áreas y volúmenes.
No hemos incluido las herramientas de construcción de circunferencias puesto que GeoGebra construye los conos y cilindros tomando como referencia los centros de las bases y el vértice en el caso del cono y abre una ventana emergente para introducir el radio.
Para los centros de las bases de los cilindros, lo mejor es dibujar un punto en el plano de la base, la recta perpendicular a dicho plano por el punto y un punto sobre esta recta. En el caso del cono procedemos de la misma manera siendo el vértice el punto sobre la recta perpendicular.