Esquema
Polyhedron as Polyhedra Generator (segments trisection)
Let the vertices of the initial polyhedron belong to the same sphere. On its basis, can be constructed a certain series of polyhedra. The vertices of each of them are the points of the trisections of the segments of the original polyhedron that have the same length (calculated with a certain accuracy). Obviously, the number of vertices of the constructed polyhedron is twice the number of trisected segments and they all lie on the same sphere.
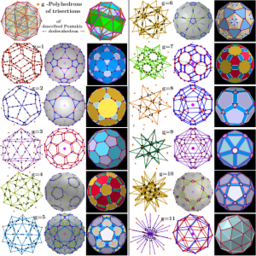
Tabla de contenidos
⓿. Biscribed Pentakis Dodecahedron
- Biscribed Pentakis Dodecahedron: The Icosahedron-Dodecahedron Compound whose all vertices lie on the same sphere
- Series of polyhedra obtained by trisection (truncation) segments of the original polyhedron
- Serie of polyhedra obtained by trisection (truncation) segments of the Biscribed Pentakis Dodecahedron
- Images. Series of polyhedra obtained by trisection (truncation) different segments of the original polyhedron
❶. Rhombicosidodecahedron (V=120) and its dual polyhedron- (V=122) from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments
- Rhombicosidodecahedron from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments
- Images . Rhombicosidodecahedron from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments
- Images 1. Rhombicosidodecahedron from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments
- Images 2. Rhombicosidodecahedron from Biscribed Pentakis Dodecahedron for the case of trisection of its 1st-order segments
❷. Truncated dodecahedron (V=60) and its dual polyhedron- Triakis icosahedron (V=32) from Biscribed Pentakis Dodecahedron for the case of trisection of its 2nd-order segments
- Truncated Dodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 2nd-order segments
- Images . Truncated dodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 2nd-order segments
- Images 1. Truncated dodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 2nd-order segments
- Images 2. Truncated dodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 2nd-order segments
❸. Truncated icosahedron (V=60) and its dual polyhedron- Pentakis dodecahedron (V=32) from Biscribed Pentakis Dodecahedron for the case of trisection of its 3rd-order segments
- Truncated Icosahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 3rd-order segments
- Images . Truncated icosahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 3rd-order segments
- Images 1. Truncated icosahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 3rd-order segments
- Images 2. Truncated icosahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 3rd-order segments
❹. Truncated icosidodecahedron (V=120) and its dual polyhedron- Disdyakis triacontahedron (V=62) from Biscribed Pentakis Dodecahedron for the case of trisection of its 4th-order segments
- Truncated icosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 4th-order segments
- Images . Truncated icosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 4th-order segments
- Images 1. Truncated icosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 4th-order segments
- Images 2. Truncated icosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 4th-order segments
❺. Polyhedron(V=120) and its dual polyhedron (V=152) from Biscribed Pentakis Dodecahedron for the case of trisection of its 5th-order segments
- Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 5th-order segments
- Images . Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 5th-order segments
- Images 1. Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 5th-order segments
- Images 2. Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 5th-order segments
❻. Polyhedron(V=120) and its dual polyhedron (V=152) from Biscribed Pentakis Dodecahedron for the case of trisection of its 6th-order segments
- Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 6th-order segments
- Images . Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 6th-order segments
- Images 1. Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 6th-order segments
- Images 2. Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 6th-order segments
❼. The Great Rhombicosidodecahedron (V=120) and its dual Disdyakis triacontahedron (V=62) from Biscribed Pentakis Dodecahedron for the case of trisection of its 7th-order segments
- The Great Rhombicosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 7th-order segments
- Images . The Great Rhombicosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 7th-order segments
- Images 1. The Great Rhombicosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 7th-order segments
- Images 2. The Great Rhombicosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 7th-order segments
❽. Rhombicosidodecahedron (V=60) and its dual Deltoidal Hexecontahedron (V=62) from Biscribed Pentakis Dodecahedron for the case of trisection of its 8th-order segments (Variant1)
- Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 8th-order segments(Variant1)
- Images . Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 8th-order segments(Variant1)
- Images 1. Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 8th-order segments(Variant1)
- Images 2. Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 8th-order segments(Variant1)
❾. Rhombicosidodecahedron (V=60) and its dual Deltoidal Hexecontahedron (V=62) from Biscribed Pentakis Dodecahedron for the case of trisection of its 9th-order segments(Variant2)
- Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 9th-order segments(Variant2)
- Images . Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 9th-order segments(Variant2)
- Images 1. Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 9th-order segments(Variant2)
❿. Polyhedron(V=120) and its dual Polyhedron(V=152) from Biscribed Pentakis Dodecahedron for the case of trisection of its 10th-order segments
- Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of a trisection of its 10th-order segments
- Images . Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of a trisection of its 10th-order segments
- Images 1. Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of a trisection of its 10th-order segments
- Images 2. Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of a trisection of its 10th-order segments
⓫. Biscribed Pentakis Dodecahedron (V=32) and its dual Biscribed Truncated Icosahedron(V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 11th-order segments