概要
Effect of GeoGebra on Learning Outcomes of Maths Students
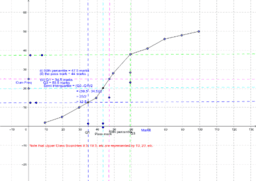
In recent times, the teaching and learning of Mathematics in Nigerian secondary schools has witnessed a great setback with students, irrespective of sex, performing poorly and showing a lack of interest. This is evident in their performance in Basic Education Certificate and Senior Secondary Certificate Examinations. The problems have been attributed partly to lack of instructional materials especially those involving Information and Communication Technology (ICT). GeoGebra, an ICT Mathematics software package for teaching Geometry, Algebra and Calculus, has been developed in response to this lack.