Teorema Fundamental do Cálculo em Análise Real
Autores: Agnaldo Esquincalha, Greice Lacerda, Thays Santos e Vinicíus Luz
Objetivo: Compreender o teorema através de manipulações no GeoGebra, aplicando em exemplos e exercícios e comparando demonstrações algébricas.
I) Partições de um intervalo
Sejam uma função limitada em [a, b] e , o conjunto dos “pontos do plano compreendidos entre o eixo das abscissas, o gráfico de f e as retas verticais e ”. (LIMA, 2013, p. 302) A área do conjunto A é um número real e pode ser calculada por aproximação (por falta ou excesso) das áreas dos polígonos retangulares P contidos em A. Neste caso, consideremos esses polígonos regulares como “reuniões de retângulos justapostos de lados paralelos aos eixos e ” (LIMA, 2013, p.303).
Observe a figura:
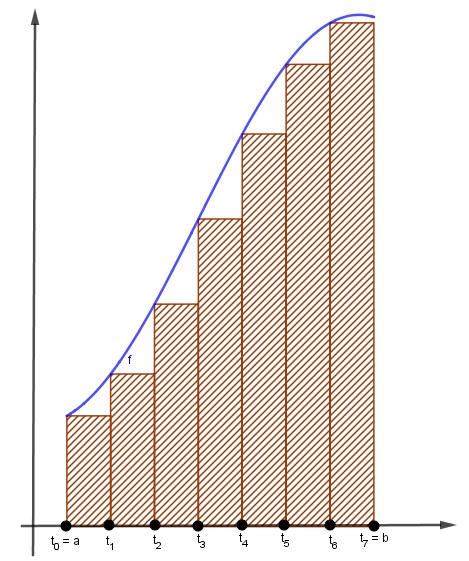
Os retângulo de base determina uma partição do intervalo [a, b] em subintervalos justapostos. Por definição, uma partição do intervalo [a, b] é um subconjunto finito tal que e . Convencionaremos sempre que . (LIMA, 2013, p.303)
II) Integral superior e integral inferior
Consideremos uma função limitada num intervalo compacto [a, b]. Sejam e , sendo o ínfimo e o supremo dos valores de f no intervalo.
Lembre-se que, por definição, uma função f: [a,b] →R é limitada num intervalo [a, b], se existem m,M números reais tais que para todo .
Ao particionarmos o intervalo [a, b] em com podemos calcular a área dos retângulos com base e alturas , , respectivamente. Note que a área desses retângulos aproxima por baixo e por cima a área da região delimitada pelo conjunto A. Quanto maior a partição, menor será o erro. Sendo assim, podemos dizer que:
A soma inferior e a soma superior da função f relativamente à partição P é definida por:
e
Se m é o ínfimo e M o supremo de f em [a,b], temos , para toda partição P do intervalo [a,b].
Quando , as somas inferior e superior, representadas por e , respectivamente, podem ser interpretadas como áreas dos retângulos inscritos e circunscritos ao gráfico de f, e portanto como valores aproximados (por falta e por excesso) da área delimitada pelo conjunto A. Toda soma inferior de f é menor ou igual a qualquer soma superior.
Observe na figura abaixo os retângulos inscritos (tracejados em vermelho) e circunscritos (em verde) ao gráfico de f:
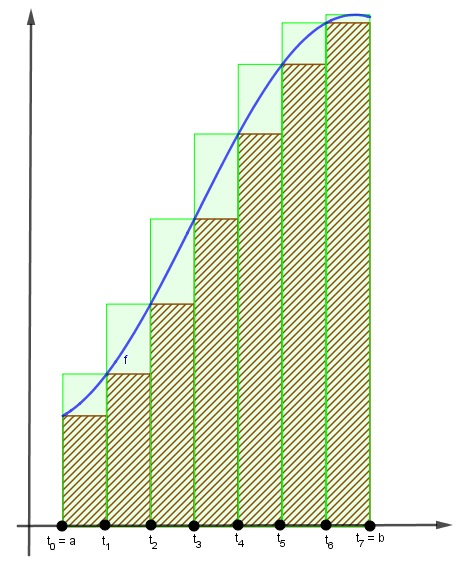

III) Funções Integráveis


Responda as questões abaixo:
a) A função g é limitada no intervalo J = [-5,10]? Justifique sua resposta.
b) Marque os botões seletores: “soma superior” e “soma inferior” e movimente os controles deslizantes c e r. O que ocorre com os valores de e à medida em que se aumenta o número de partições do intervalo [a, b]?
c) Podemos afirmar que a função g é integrável no intervalo [a, b] dado? Justifique sua resposta.
d) Descreva como seria a integral dessa função.
Exemplo 2:
Considere as funções , tal que . 1º passo: Movimente os controles deslizantes a e b e escolha um intervalo [a, b] de sua preferência. 2º passo: Movimente livremente o controle deslizante n, observe as funções geradas, escolha uma função e responda as perguntas abaixo:
a) Qual foi a função escolhida?
b) Qual foi o intervalo [a, b] escolhido?
c) Marque as caixas: “soma superior” e “soma inferior” e movimente o controle deslizante r. O que ocorre com os valores de e à medida que se aumenta o número de partições do intervalo [a, b]?
d) A função h escolhida é integrável no intervalo [a, b] escolhido? Justifique sua resposta.
e) Se a resposta ao item anterior foi positiva, determine um intervalo no qual a função h escolhida não seja integrável. Se foi negativa, escolha um intervalo no qual h seja integrável. Justifique sua resposta.
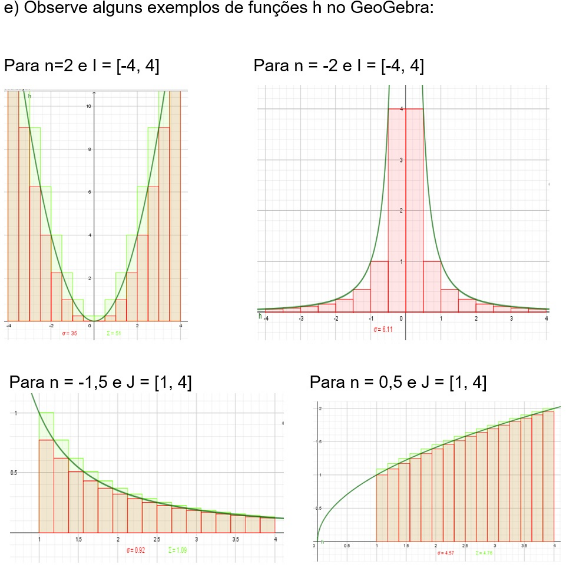
Tente reproduzi-las no GeoGebra e responda a pergunta abaixo:
IV) Teorema fundamental do Cálculo (TFC)
Segundo Lima (2013):
TFC (versão 1): Se uma função integrável possui uma primitiva , então .
ou ainda,
TFC (versão 2): Se uma função possui uma derivada integrável, então .
Neste exemplo vamos utilizar, além da janela de álgebra, a janela Cálculo Simbólico (CAS).
1º passo: Movimente os controles deslizantes para a = 2 e b = 4. Na janela de CAS, observe os valores de F(b) – F(a) e c. E na janela de álgebra, observe os valores de e .
a) Podemos afirmar que f é integrável no intervalo [a, b]? Justifique sua resposta.
b) Para a função f no intervalo [2, 4] poderemos aplicar o TFC? Justifique sua resposta.
2º passo: Movimente os controles deslizantes para a = 2.1, b = 3.
c) Na janela de CAS, observe os valores de F(b) – F(a) e c. E na janela de álgebra, observe os valores de e . Selecione as caixas de “soma superior” e “soma inferior”, movimente o controle deslizante r para valores maiores que 1000. Observe os valores de: , , F(b) – F(a) e c. Podemos aplicar o TFC na função f no intervalo [2.1, 3]? Justifique sua afirmação a partir da definição do teorema.
3º passo: Escolha outros valores para a e b.
d) Podemos afirmar que a função f satisfaz as condições do TFC no intervalo [a, b] que você escolheu? Justifique sua resposta.
e) A partir dos itens anteriores, como você justificaria o Teorema Fundamental do Cálculo?.
f) A partir da justificativa dada no item anterior, esboce uma demonstração do TFC.
Enriquecendo a Aprendizagem.

