Kapitel
Le jeu de dobble
Dans le jeu de Dobble, on a des cartes sur lesquelles sont représentés des symboles. Chaque paire de cartes a toujours exactement un symbole en commun et un seul. De plus, si vous prenez deux symboles, il n'existe qu'une seule carte les contenant tous les deux. Cette magie tient à la géométrie projective sur un corps fini: , l'ensemble des entiers modulo un nombre premier, a une structure de corps. On peut étudier les droites dans le plan fini , il y a points donnés par leurs coordonnées chacune entre 0 et . Il y a droites vectorielles, de la forme pour chaque et la verticale .
Chacune a points (l'origine est commune à toutes ces droites vectorielles).
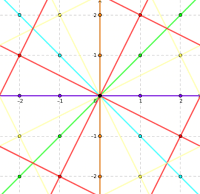
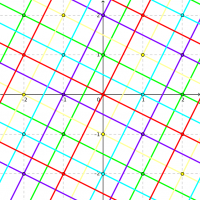
En translatant ces droites afin qu'elles ne passent plus par l'origine, on obtient droites affines, qu'on peut aussi comptabiliser par leurs équations cartésiennes , , et non nuls simultanément, et définis uniquement à un multiple non nul près. Cela donne . Mais deux droites de même direction sont parallèles, elles ne se coupent pas (ou bien sont confondues).
Pour chacune des directions, on complète le plan fini par un point à l'infini, qui est le point "commun" à chacune des droites parallèles de même direction. Il y a donc points à l'infini et le plan projectif a points, qui définissent , autant de droites affines de chacune points.
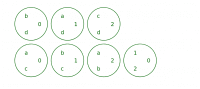
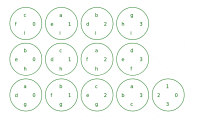
On a donc en tout symboles, autant de cartes, de chacune symboles.
Remarquons la symétrie de dualité entre les points et les droites dans cet espace projectif.