Reflection
A reflection is a geometric transformation that reverses the position of an object concerning a plane, line, or specific point. In a reflection, the points of the object are mirrored concerning the geometric reflection element, meaning the distance of each point to the element is preserved, but its position relative to that element is inverted.
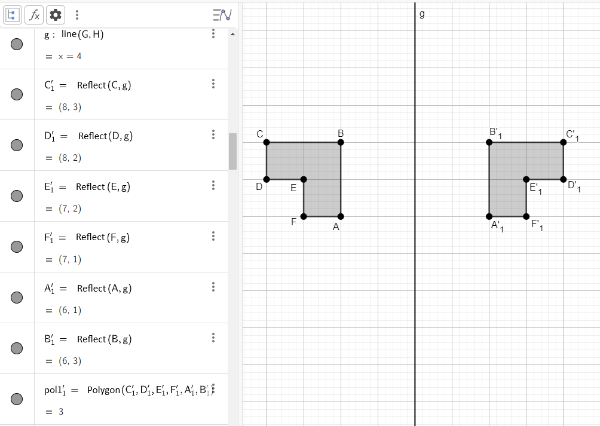
In Figure 2, we observe the polygon A'1B'1C'1D'1E'1F'1 as the result of the reflection of polygon ABCDEF concerning line r.
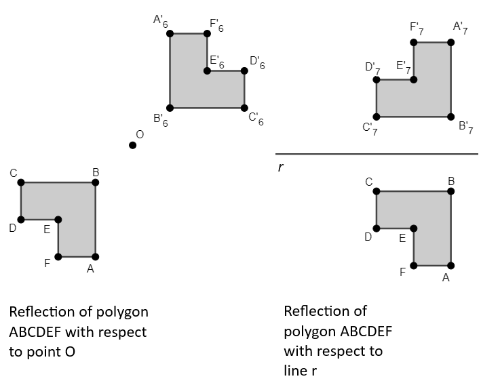
Other possible reflections of polygon ABCDEF can be seen in Figure 7.
Figure 7 – Reflection of polygon ABCDEF concerning different geometric objects.
In GeoGebra, the command used to perform reflections is the Reflection command when using the English version. The available reflection options include reflection concerning a point, a line, a plane, or a circle. In this work, we will focus on the options reflection concerning a point and reflection concerning a line.
To carry out an activity involving the reflection of a polygon, access the GeoGebra Geometry application through the link https://www.geogebra.org/geometry/fzu5kbcd and follow the proposed steps:
- Insert points A, B, C, D, E, and F in the Cartesian plane
 .
. - Create polygon ABCDEF using the inserted points
 .
. - Create a line through two other points
 .
. - Perform the reflection of polygon ABCDEF concerning the created line. To do this, in the Input Field of the Algebra Window, you can use the command
Reflection(object, line), where the selected object should be polygon ABCDEF (pol1), and the line should be the created line (g). Another way is to use the Reflection over a Line button .
.
pol1), GeoGebra automatically reflects all points and all segments of the polygon to generate the new polygon A’₁B’₁C’₁D’₁E’₁F’₁ (pol1’₁).