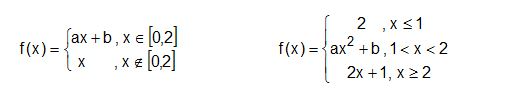Definition
![[size=100]Die Stetigkeit einer Funktion an einer bestimmten Stelle ist eine lokale Eigenschaft, d.h. eine Eigenschaft der Funktion, die sich auf einen bestimmten Punkt, auf einen bestimmten x – Wert x[sub]0[/sub] bezieht.
x – Werte, für die eine Funktion nicht stetig ist, heissen Unstetigkeitsstellen; die Funktion heisst an dieser Stelle unstetig.
[/size]](https://www.geogebra.org/resource/sgydhq7m/pXy0T0ll5RmqtcMY/material-sgydhq7m.png)
Arbeitsauftrag 1
Untersuche alle Funktionstypen, die wir kennen gelernt haben, auf Stetigkeit bzw. Unstetigkeit.
Arbeitsauftrag 2
Gegeben seien die beiden folgenden Funktionen: f1(x) = 3x und f2(x) = .
Skizziere die Grafen der beiden Funktionen. Erkläre!
Übung 1
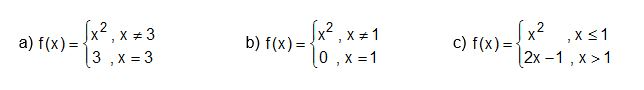
Übung 2
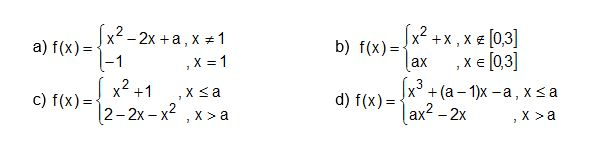
Übung 3