Part 3: Prove

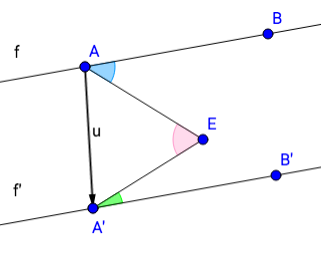
Strategy You observed the given diagram, then made a conjecture. Then you built a model and gathered some data. That may have caused you to rethink your conjecture somewhat--or perhaps it strengthened your conviction. Either way, by this phase you should have a conjecture that you truly believe in. The goal now is to demonstrate or prove your conjecture. Does measuring angles prove whether or not angles are congruent? What does? You can use any geometric tools, working on paper and/or in geogebra to try and find a way of demonstrating your conjecture. Two-Column Proof Now you've developed a way to demonstrate that your conjecture is true. A proof is how you clearly present your solution. It begins with the problem as it is given to you. From there, you take one logical step at a time towards the conclusion you want to show is true. In this case, the conclusion you want to prove true is your conjecture. Complete the proof in two-column form.