Praktikum - Kongruenzsätze von Dreiecken
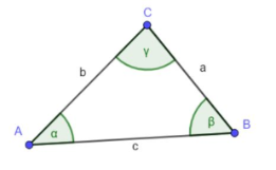
Wdh.: Allgemeine Beschriftung von Dreiecken und Vierecken
Lernziele des Praktikums sind:
Verschieben von Objekten.
Setzen eines beliebigen Punktes
Markieren des Schnittpunkts zweier Linien
Zeichnen einer Gerade durch zwei Punkte.
Zeichnen eines Kreises mit gegebenem Mittelpunkt sowie einem weiteren Punkt, durch den er geht.
Zeichnen eines Kreises mit gegebenem Mittelpunkt und Radius.
Zeichnen eines Winkels mit festgelegtem Winkelmaß.
Zeichnen der Strecke zwischen zwei Punkten.
- Sicheres Konstruieren von Dreiecken nach verschiedenen Kongruenzsätzen.
- Erkenntnis, warum es beim Kongruenzsatz Ssw wichtig ist, dass die kürzere Seite am gegebenen Winkel anliegt.
Verschieben von Objekten.
Setzen eines beliebigen Punktes
Markieren des Schnittpunkts zweier Linien
Zeichnen einer Gerade durch zwei Punkte.
Zeichnen eines Kreises mit gegebenem Mittelpunkt sowie einem weiteren Punkt, durch den er geht.
Zeichnen eines Kreises mit gegebenem Mittelpunkt und Radius.
Zeichnen eines Winkels mit festgelegtem Winkelmaß.
Zeichnen der Strecke zwischen zwei Punkten.Aufgabe 1
Bearbeite die Aufgabe mit einem Partner oder einer Partnerin. Es soll ein Geometriediktat durchgeführt werden. Dazu gibt Partner*in A in kleinen Schritten Anweisungen, die Partner*in B im folgenden Applet durchführt. So wird ein eindeutiges Viereck konstruiert. Die gegebenen Größen findet Partner*in A, in dem er/sie den Abschnitt "Konstuktionsanweisung" markiert.
Nachdem das erste Viereck konstruiert wurde, könnt ihr die Rollen vertauschen und das zweite Viereck konstruieren.
Konstruktionsanweisung 1:
a = 3LE
b = 4,5LE
=
118°
= 20°
= 190°
Konstruktionsanweisung 2:
= 32°
a = 6LE
b = 1,5LE
c = 4LE
d = 5,5LENach welchen Kongruenzsätzen für Dreiecke ist das erste Viereck unter den gegebenen Angaben eindeutig konstruierbar?
Nach welchen Kongruenzsätzen für Dreiecke ist das zweite Viereck unter den gegebenen Angaben eindeutig konstruierbar?
Was ist dir schwergefallen, als du gezeichnet hast?
Was waren deine Schwierigkeiten beim Konstruktionsanweisungen geben?
Aufgabe 2
a) Arbeite jetzt in Einzelarbeit. Konsturiere aus den Angaben a = 6LE, b = 4LE und = 30° alle möglichen Dreiecke.
Sind alle konstruierten Dreiecke kongruent?
b) Welche Angaben aus Aufgabenteil a) kannst du bspw. ändern, sodass die Dreieckskonstuktion eindeutig ist? Verifiziere deine Antwort, indem du alle möglichen Dreiecke aus diesen Angaben konstruierst und überprüfst, ob sie kongruent sind.
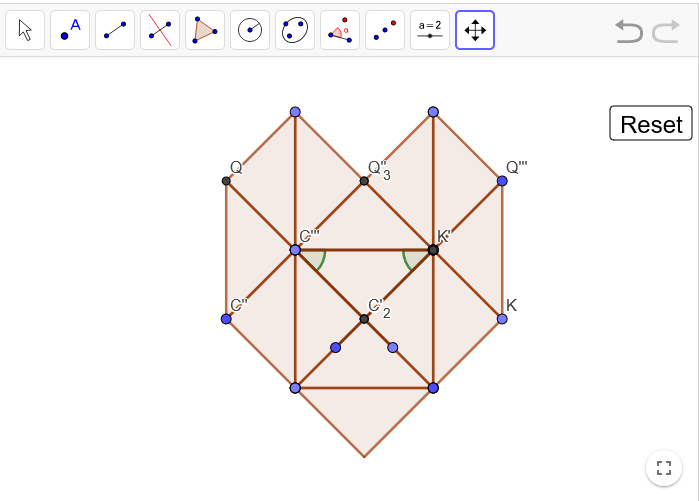
Bonusaufgabe
Probiere dich in den Werkzeugen aus und probiere, das Herz aus kongruenten Dreiecken zu rekonstruieren. Nutze zum Beispiel "Drehe um Punkt" und "Verschiebe um Vektor".
