花火のようにはじける
このワークシートはMath by Codeの一部です。
アート、背景、実装、バリエーションの順に見ていきましょう。

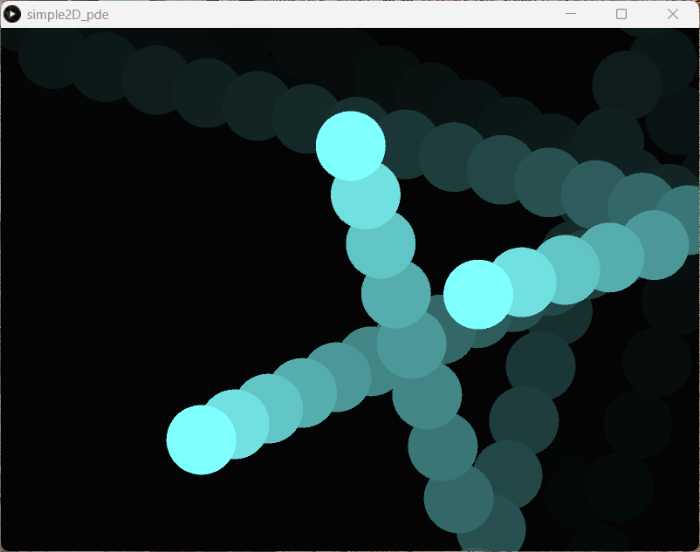
1.背景
実際の玉に近い動きを2Dで再現しています。
玉を大きくして、個数を減らすと動きの規則がよくわかります。
上の絵は花火っぽいですが、
下の絵は円板っぽいですね。
玉は中央から発射されて、適当な加速度ベクトルに重力がたされた速さで動き出します。
そのあとは、重量加速度だけかかりので等加速度運動になり、枠にぶつかると反射しながら、どんどん地面に落ちていきます。
玉のもつ特徴を「性質と動き」にわけて記述することで、
玉の変化をコード化しやすくなります。
昔から、シミュレーションというのは物理の世界ではよくありましたが、
設定を現実以上の数値にしたりすることで、アート作品を作ることにもつながるようです。
それを人の入力や動きなどへ応答する、インタラクティブな仕組みをくっつければ、
立派な体験型のアートが作れるでしょう。
今回のテーマは「物の運動のコード化」と「クラスプログラミング」です。
<等加速度運動の運動方程式>
運動方程式というと、すごい威圧感を感じる人もいるかもしれません。
しかし、運動方程式は、
しかし、ボールがもっている運動の状態の特性量、
(人間でいうと身長、体重、体温、血圧、血糖値のような基本特性)
こられの特性量が、時間やイベントでどう変化するかをイメージする基本の道具です。
ボールの運動状態の特性に関係あるものをならべましょう。
加速度accel
重力g
速度v
位置pos
ある場所から放出する加速度がaccel=aだとしよう。
(ここから毎秒更新)
これから1秒ずつ、特性量は更新されます。
放出しても重力がかかるので、加速度accel=accel+gとします。
速度はaccelだけ加速されますね。v=v+accelとします。
位置は速さvだけ進みます。pos=pos+vとします。
重力以外に加算される加速度はないので、
accel=0にしてから、毎秒更新の上から実行します。
直線上の動きならどうなるでしょうか。
地面から加速度aで真上に投げ上げた(これを正方向)とすると、横軸tでの変化は、
加速度は、投げ上げの瞬間だけaccel=a あとはずっとaccel=-g
速度は、投げ上げの瞬間はv(t)=a あとは、毎秒-gがたされます。
時間に比例して速さは減っていくので、投げてからt秒後の速度はtの1次関数になるね。
縦軸v、横軸tのグラフで表示しよう。
v(t)=a-gt(上底a 、下底 a-gt, 高さtの台形のグラフ)
このv(t)を時間で積分したものが道のりの増加、
積分は、たて切りした短冊の面積の合計だから、
台形の面積になる。
pos(t)=pos+v(t)の台形の面積=pos+(初速度+t秒後の速度)×経過時間/2
pos+(a+a-gt) t /2=pos + at- gt2/2
斜めに動かす場合は、上下方向だけ投げ上げと同じ式になり、
左右方向は斜めに投げたときの加速で決まった速度のまま進みます。
壁に跳ね返りなが進むときは、壁から力がかかり、反作用で壁に押される力がかかります。
しかし、それはぶつかった瞬間に加速度を生みますが、離れてしまえば等速です。
だから、簡単のために壁にぶつかったときは、それ以上増減できない方向での速度成分だけ、
向きを反転させればよいですね。
先の方まで、数式化しようとすると、大変なことに思えるかもしれません。
しかし、瞬間ごとの変化、
ひらたく言えば1秒後の変化がどうなるか、コマ送りでイメージすると、
運動方程式というものが、
とても、簡単な内容を言っているだけだと気づくでしょう。
さいしょは、運動に関係のある特性の量を上下方向だけの数値としてイメージしました。
しかし、これをベクトルとしてとらえてもよいでしょう。
ベクトルとみなすと、
画面にかく用途以外では2Dでも3Dでも記述に差がなくなるので、楽になるのです。
<クラスプログラミング>
ヒトに身長、体重、体温、血圧、血糖値のような基本特性があり、
いろんなイベントによって変化するように、
ボールにも属性があって、時間経過というイベントや壁との衝突というイベントで変化します。
1人ひとりは具体ですが、ヒトというのは抽象的な型です。
1つひとつのボールは具体ですが、ボールの属性リストと変化の仕方は抽象的な型です。
この抽象的な型のことをクラス、それにあてはまる具体をインスタンスといいます。
クラスをかいておくと、冒頭の花火のような動きは、個数を5にしても300にしても
インスタンス数だけ変えるだけで、他は特に変える必要ありません。
このようにクラスとインスタンス、抽象と具体という2層に分けるプログラミングの方向性を
オブジェクト指向と呼んだりします。
クラスにはインスタンス属性(特性、プロパティー)と属性設定関数(メソッド)があります。
クラス中心を使いこなすためには、
継承や関数の多態性や多重定義、インターフェース、
堅牢性と柔軟性、オープンとプライベート、秘匿性
などなど、
いろんな発想や概念や流儀があり、
きりがないので深く掘り下げることはしません。
クラスという書き方の1種があるという程度の説明だと思って読んでください。
<クラスプログラミングの基本は3項目>
クラス定義に不可欠な
・コンストラクターという関数設定で、具体を生むときの属性を初期化するかき方。
・インスタンスの属性を変えるためのメソッドとしての関数設定の仕方。
クラス利用に不可欠な
・クラスのインスタンスの宣言と初期化の書き方。
質問:先のボールの位置posの初期化と更新を手続き的ではなく、クラスとしてコード化するにはどうしたらよいでしょう。
2.実装
<Python>
・はじめはクラス定義からです。
class クラス名(list):から始めます。
( )ではなく、(list)にしているのは、listクラスを継承して複数の具体(ボール)をリスト化するためです。
・コンストラクター関数は、特に読み込む数値がなければ、def _init_(self):
というお決まりのセリフから始めます。
たとえば、ボールの半径をr=4.0にしたいなら、self.r=4.0のように、必ず[self.]を変数名につけて、
ただの変数ではなくて、クラスのインスタンスの属性だとわかるようにするのですね。
こうして、半径r, 質量mass, 加速度accel、速度v, 空気摩擦率 frict, 位置 pos
をどんなボールにも共通の初期化ができるようにします。
PVector型はprocessing用のベクトルの型名です。
コンストラクターに限らす、クラスで決めるインスタンス用の関数は(self)にしてselfを呼び込みましょう。
・update関数は、先ほどのaccel にgをたして加速度にしてvにたす。そして、vを空気摩擦率だけ遅くしてから、位置posにvをたしましょう。最後に加速度は0にしておき、重力以外の加速度がたされないようにします。fill(H,S,B)モードで指定して1個ずつ色を指定します。カラフルになるように値を明るさB以外をランダムにすればいいね。ellipseでかく位置とサイズを指定します。最後に、壁にバウンドしたときの向きの反転を書いときます。これで、クラスPVec2型ができました。クラス定義は別ファイルにかいて、使いまわしをすることが多いのですが同一でも構いません。
・次はクラス利用です。
NUMで粒子数、particlesで粒子リストにして、
setup関数の中で、part = PVec2()で1個のインスタンスを作ります。
その属性をバラバラに呼び出してもよいのですが、セット用の関数
インスタンス.属性名.set(属性値)という構文でセットできます。
part.posは画面中央ですが、part.accelがランダムなので、四方八方に適当に散りますね。
設定するたびに、particlesリストにpartを登録していきます。
draw関数の中で、背景をfill(0,0,0,0.125)でα値を12.5%にすることで、残像を生む設定にして
rect(0, 0, width, height)で画面を塗ってから、粒子を描画するようにしています。
1個ずつのparticles[i]に対して、クラスで決めたインスタンス関数updateを実行しています。
だから、1個ずつ色が異なり、瞬間瞬間、色が変わります
class PVec2(list):
#constructor to make instance
def __init__(self):
self.r = 4.0
self.mass = 1.0
self.accel = PVector(0.0, 0.0)
self.v = PVector(0.0, 0.0)
self.frict = 0.01
self.pos = PVector(0.0, 0.0)
def update(self):
self.accel.add(PVector(0.0, 0.1))
self.v.add(self.accel)
self.v.mult(1.0 - self.frict)
self.pos.add(self.v)
self.accel.set(0, 0)
fill(random(1),random(1),0.9)
ellipse(self.pos.x, self.pos.y, self.mass * self.r * 2, self.mass * self.r * 2)
#reflection
if self.pos.x > width:
self.pos.x = width
self.v.x *= -1
if self.pos.x < 0.0:
self.pos.x = 0.0
self.v.x *= -1
if self.pos.y > height:
self.pos.y = height
self.v.y *= -1
if self.pos.y < 0.0:
self.pos.y = 0.0
self.v.y *= -1
NUM = 300
particles = []
def setup():
size(800, 600, P2D)
frameRate(60)
for i in range(NUM):
part = PVec2()
part.pos.set(width/2.0, height/2.0)
angle = random(PI * 2.0);
leng = random(20);
part.accel.set(cos(angle) * leng, sin(angle) * leng);
particles.append(part)
colorMode(HSB, 1,1,1,1)
def draw():
#backgroud
# 0,0,0 for black and 0.125 alpha for afterimage
fill(0,0,0,0.125);
rect(0, 0, width, height);
noStroke()
for i in range(NUM):
particles[i].update()
<P5.js>
P5.jsはp5.js Web Editor
でインストールなしで実行できます。
(ただし、ファイルとして保存するには、アカウントをメールアドレスを登録するか
googleアカウントなどを利用して、ログインが必要です。)
python in processingとの違いは、形式的な部分だけです。
selfの代わりに、thisにして、PVectorの代わりにcreateVectorにします。
constructorは、まんまの名前でわかりやすいですね。pythonより。
しかも、クラス定義の中の関数定義はfunction というタイプ名も不要で、とてもシンプルです。
class PVec2 {
constructor() {
this.r = 4.0;
this.mass = 1.0;
this.frict = 0.01;
this.pos = createVector(0.0, 0.0);
this.v = createVector(0.0, 0.0);
this.accel = createVector(0.0, 0.0);
}
update() {
this.accel.add(createVector(0.0, 0.1));
this.v.add(this.accel);
this.v.mult(1.0 - this.frict);
this.pos.add(this.v);
this.accel.set(0, 0);
fill(random(1),random(1),0.9)
ellipse(this.pos.x, this.pos.y, this.mass * this.r * 2, this.mass * this.r * 2);
if (this.pos.x > width) {
this.pos.x = width;
this.v.x *= -1;
}
if (this.pos.x < 0.0) {
this.pos.x = 0.0;
this.v.x *= -1;
}
if (this.pos.y > height) {
this.pos.y = height;
this.v.y *= -1;
}
if (this.pos.y < 0.0) {
this.pos.y = 0.0;
this.v.y *= -1;
}
}
}
const NUM = 1000;
part = [];
function setup() {
createCanvas(800, 600, P2D);
frameRate(60);
for (let i = 0; i < NUM; i++) {
part[i] = new PVec2();
part[i].pos.set(width/2.0, height/2.0);
angle = random(PI * 2.0);
leng = random(20);
part[i].accel.set(cos(angle) * leng, sin(angle) * leng);
part[i].frict = 0.01;
}
colorMode(HSB, 1,1,1,1);
}
function draw() {
fill(0,0,0,0.125);
rect(0, 0, width, height);
noStroke();
fill(0.5,0.5,1);
for (let i = 0; i < NUM; i++) {
part[i].update();
}
}
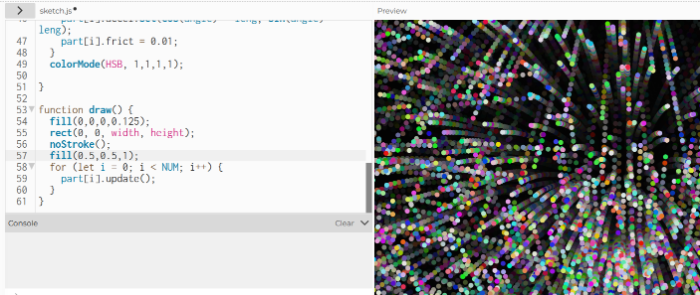
3.バリエーション
今回は、geogebraの開発環境について実験してみましょう。
geogebraのアプレットの開発でよくあるのは、
メニューから貼り付けたり、
数式に1行単位でコマンドを入れることです。
「スクリプト記述」というものをすると、さらに自由度が広がりますが、
geogebraのスクリプトにして、javascriptのスクリプトにしても、
オブジェクトを右クリックして、オブジェクトごとにコードを入れるという手間がかかります。
あまり、効率的ではありません。
エラーが出ても、エディターがないのでバグとりも大変です。
そこで、今回はHtmlファイルにjavascriptによってgeogebraアプレットを差し込む
という開発環境を実行してみよう。
<環境作り>
htmlファイルとscrip.jsを同じフォルダにおきましょう。
埋め込みたいjsはscript.jsという名前にしてあります。
VSコードで、この2つのファイルのあるフォルダをひらきます。
htmlファイルを右クリックして、open live serverとすると、
htmlの中に埋め込まれたgeogebraアプレットが開きます。
開いたブラウザーのその他のツールなどのデベロッパーツールなどを開くと、
エラーの有無やconsole.log()の結果が表示されて、ソースなども確認できます。
(この環境のよいところ)
ES2015というモダンな書き方ができる点がよいです。
・const とletの使い分けができる。
・テンプレート文字列が使えるので視認性がよくなった。
従来の書き方
g.evalCommand("s" + count+ "=Vector(Point({" +(j+2)+ "," +count+"}),Point({" +(j+1)+ "," +count+"}))");
テンプレート文字列を使う書き方
let temp=`s${count}=Vector( Point( {${j+2}, ${count}} ) , Point( {${j+1) , ${count}} ) )`;
g.evalCommand(temp);のように、呪文っぽい読みずらさがかなり軽減する。
クラスがgeogebraのアプレットで使える。
クラスを使うコードはjavascriptでかけますが、メモ帳でかくとデバックできません。
この環境でかいたスクリプトはconsole.log()を挿入することで、どこまで、どう動いたかが
webブラウザのデベロッパーズツールで表示できる。
どこがエラーか、なぜエラーかがはっきりわかる。
もちろん、カッコの対応やカッコの種類のミスなどは簡単に排除できます。
(この環境のよくないところ)
jsの最初のパラメータ設定の部分は、自明な部分でも多数の記述になっている点が冗長だし、
ぱっと見で、とても難解に見える。
ただ、ふだん見慣れていないDOMやイベントリスナー(アプレットの応答)の設定を
省略なしの命名規約に従って記述しなければならないだけのことです。
名前自体が親切な説明になっているんだと、割り切るしかないですね。
vector型とかタプル型がないので、座標にわけて[0][1]のようにつけて、処理する点がとても行数が増えて冗長。もちろん、vectorクラスを定義してしまえば問題ないが、手間です。
index.html

#======== script.js================
// GeoGebra Appletのパラメータ設定
const params = {
"appName": "classic", // または "geometry", "graphing" など
"width": 800,
"height": 600,
"showToolBar": true, // ツールバー
"showMenuBar": true, // メニューバー
"showAlgebraInput": true, // 代数入力欄
"showResetIcon": true, // リセットアイコン
"enableLabelDrags": false,
"enableShiftDragZoom": true,
"capturingThreshold": 3,
"showTutorialLink": true,
"showContextMenu": true,
"scaleContainerClass": "applet_container", // アプレットを埋め込むHTML要素のID
//"filename": "part2.ggb", // .ggbファイルを読み込む場合
// "ggbBase64": "...", // .ggbファイルをBase64文字列で直接埋め込む場合
// Appletのロード
"appletOnLoad": function(applet) {
window.ggbApplet = applet; // グローバル変数にappletオブジェクトを保存
console.log("GeoGebra Appletがロードされました");
document.getElementById('resetButton').addEventListener('click', setupPoints);
document.getElementById('startButton').addEventListener('click', startAnimation);
document.getElementById('stopButton').addEventListener('click', stopAnimation);
setupPoints();
}
};
// GeoGebra Appletを初期化して、指定されたコンテナに埋め込む
// deployggb.js によって提供される GGBApplet クラスを使用
const applet = new GGBApplet(params, true); // true はマテリアルIDを使用しない意味
// DOMContentLoaded イベントでアプレットを書き込む
window.addEventListener('DOMContentLoaded', function () {
applet.inject('applet_container'); // 'applet_container' はHTMLのdiv要素のID
});
let particles = []; // パーティクル
let animationInterval; // アニメーションのインターバルID
class PVec2 {
constructor() {
this.r = 0.5;
this.pos = [0.0, 0.0];
this.v = [0.0, 0.0];
this.accel = [0.0, 0.0];
this.colr=255;
this.colg=255;
this.colb=255;
this.xMin = -5.0;
this.xMax = 5.0;
this.yMin = -5.0;
this.yMax = 5.0;
}
update() {
this.accel[1] -= 1.0;
this.v[0] += this.accel[0];
this.v[1] += this.accel[1];
this.pos[0] += this.v[0];
this.pos[1] += this.v[1];
this.accel = [0, 0];
this.colr= Math.random() * 255;
this.colg= Math.random() * 255;
this.colb= Math.random() * 255;
if (this.pos[0] > this.xMax) {
this.pos[0] = this.xMax;
this.v[0] *= -0.9;
}
if (this.pos[0] < this.xMin) {
this.pos[0] = this.xMin;
this.v[0] *= -0.9;
}
if (this.pos[1] > this.yMax) {
this.pos[1] = this.yMax;
this.v[1] *= -0.9;
}
if (this.pos[1] < this.yMin) {
this.pos[1] = this.yMin;
this.v[1] *= -0.7;
}
}
}
function setupPoints() {
// 既存の点pオブジェクトあれば削除
if (particles.length > 0) {
for (let i = 0; i < particles.length; i++) {
window.ggbApplet.deleteObject("p" + i);
}
}
particles = [];
const NUM = 100;
for (let i = 0; i < NUM; i++) {
let part = new PVec2();
part.pos = [0 , 0 ];
let angle = Math.random() * Math.PI * 2.0;
let leng = Math.random() * 6.0;
part.accel = [Math.cos(angle) * leng, Math.sin(angle) * leng];
part.colr= Math.random() * 255;
part.colg= Math.random() * 255;
part.colb= Math.random() * 255;
particles.push(part);
let posinfo = `p${i}=Point({${part.pos[0]},${part.pos[1]}})`;
window.ggbApplet.evalCommand(posinfo);
window.ggbApplet.setColor("p" + i, part.colr, part.colg, part.colb);
window.ggbApplet.setLabelVisible("p" + i,false);//NO label
window.ggbApplet.setAxesVisible(false,false);//No Axes
window.ggbApplet.setGridVisible(false);//No Grid
}
drawPoints(); // 初期位置を描画
}
// アニメーションループ関数
function drawPoints() {
if (particles.length === 0) return; // パーティクルがない場合は何もしない
for (let i = 0; i < particles.length; i++) {
let part = particles[i];
let posinfo = `p${i}=Point({${part.pos[0]},${part.pos[1]}})`;
window.ggbApplet.evalCommand(posinfo);
this.colr= Math.random() * 255;
this.colg= Math.random() * 255;
this.colb= Math.random() * 255;
window.ggbApplet.setColor("p" + i, part.colr, part.colg, part.colb);
part.update();
}
}
// アニメーション開始
function startAnimation() {
if (animationInterval) {
clearInterval(animationInterval); // 既存のアニメーションがあれば停止
}
// 180fps (約200msごとに実行)
animationInterval = setInterval(drawPoints, 200);
}
// アニメーション停止
function stopAnimation() {
if (animationInterval) {
clearInterval(animationInterval);
animationInterval = null;
}
}
質問:このweb埋め込みでうまくいった部分を、埋め込みなしのgeogebraアプレットに改造するにはどうしたらよいでしょう。
基本は「スクリプト記述」の「グルーバルjavaスクリプト」の空白にクラスの設定と、その利用部分を貼り付けます。
タイマーがないので、スライダーを貼り付けます。
スラーダーの「最新情報」(onUpdate)にdrawPoints();とかき、種類をjavascriptにします。
また、ボタンをつけて、StartAnimation[]やStartAnimation[false]などのスクリプト記述を「クリックして」(OnClicked)にかきましょう。(これはGeogebraScript)
resetボタンは「クリックして」にsetupPoints();をjavascriptにしていれます。
最後に、「完了」ボタンを押して、上に保存してから閉じて、もう一度開き直さないと、
更新した状態が上書きされずに、表面的な変更になるのでここでも、エラーが起きたりします。
ただし、埋め込みのための呪文のようなパラメータ記述は不要になります。
ggbAppletのオブジェクト名は通常gにしますが、変更が面倒だったので、
埋め込み型のときの名前window.ggbAppletをドットをとったwindowggbAppletにしています。
//グルーバルjavaスクリプト
let windowggbApplet = ggbApplet;
let particles = []; // パーティクル
function ggbOnInit() {
setupPoints();
}
class PVec2 {
constructor() {
this.r = 0.5;
this.pos = [0.0, 0.0];
this.v = [0.0, 0.0];
this.accel = [0.0, 0.0];
this.colr=255;
this.colg=255;
this.colb=255;
this.xMin = -5.0;
this.xMax = 5.0;
this.yMin = -5.0;
this.yMax = 5.0;
}
update() {
this.accel[1] -= 1.0;
this.v[0] += this.accel[0];
this.v[1] += this.accel[1];
this.pos[0] += this.v[0];
this.pos[1] += this.v[1];
this.accel = [0, 0];
this.colr= Math.random() * 255;
this.colg= Math.random() * 255;
this.colb= Math.random() * 255;
if (this.pos[0] > this.xMax) {
this.pos[0] = this.xMax;
this.v[0] *= -0.9;
}
if (this.pos[0] < this.xMin) {
this.pos[0] = this.xMin;
this.v[0] *= -0.9;
}
if (this.pos[1] > this.yMax) {
this.pos[1] = this.yMax;
this.v[1] *= -0.9;
}
if (this.pos[1] < this.yMin) {
this.pos[1] = this.yMin;
this.v[1] *= -0.7;
}
}
}
function setupPoints() {
// 既存オブジェクトあれば削除
if (particles.length > 0) {
for (let i = 0; i < particles.length; i++) {
windowggbApplet.deleteObject("p" + i);
}
}
particles = [];
const NUM = 100;
for (let i = 0; i < NUM; i++) {
let part = new PVec2();
part.pos = [0 , 0 ];
let angle = Math.random() * Math.PI * 2.0;
let leng = Math.random() * 6.0;
part.accel = [Math.cos(angle) * leng, Math.sin(angle) * leng];
part.colr= Math.random() * 255;
part.colg= Math.random() * 255;
part.colb= Math.random() * 255;
particles.push(part);
let posinfo = `p${i}=Point({${part.pos[0]},${part.pos[1]}})`;
windowggbApplet.evalCommand(posinfo);
windowggbApplet.setColor("p" + i, part.colr, part.colg, part.colb);
windowggbApplet.setLabelVisible("p" + i,false);//NO label
windowggbApplet.setAxesVisible(false,false);//No Axes
windowggbApplet.setGridVisible(false);//No Grid
}
drawPoints();
}
function drawPoints() {
if (particles.length === 0) return; // パーティクルがない場合は何もしない
for (let i = 0; i < particles.length; i++) {
let part = particles[i];
let posinfo = `p${i}=Point({${part.pos[0]},${part.pos[1]}})`;
windowggbApplet.evalCommand(posinfo);
this.colr= Math.random() * 255;
this.colg= Math.random() * 255;
this.colb= Math.random() * 255;
windowggbApplet.setColor("p" + i, part.colr, part.colg, part.colb);
part.update();
}
}