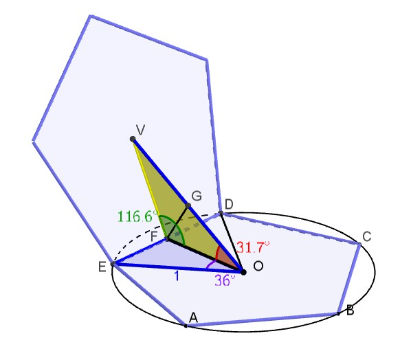
trigonomic calculation
distance between the centers of gravity of adjacent faces
- Create a regular pentagon inscribed in a circle with radius 1.
- In this pentagon .
- FOV is an isoscleles triangle with .
- In this triangle
- The distance between the centers of gravity O and V equals .
distance bewteen the centers of gravity of faces connected to each other by one face
- In the dodecahedron .
- The centers of gravity O, V and W form an isosceles triangle with and .
- In this triangle
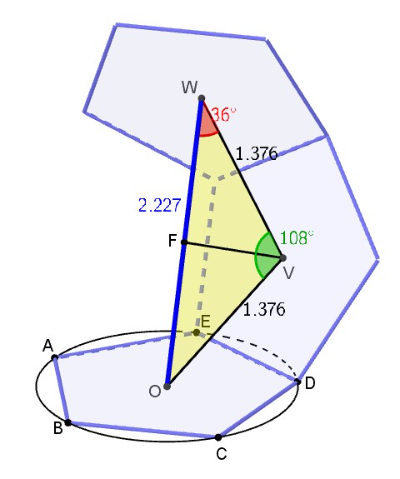
proportion of this two distances
The angle between [OV] and [VW] equals 108°, so =36°.
The cosine of 36° equals or .
Since you can also write .
Conclusion: the fascination of the admirers of the Golden Section for the fact that in a dodecahedron one can draw three Golden Rectangles perpendicular to each other can be reduced to a simple geometric property:
- First define the centers of gravity of three faces: two adjacent faces and a third one, adjacend to the second face but not to the first one.
- Construct an angle with vertex the center of gravity of the first face and legs the segments that connect this point to the other two points.
- Constatation: The constructed angle in the center of gravity of the first face equals 36°.