Vektoren im Raum
Vektoren
Ein Vektor gibt dir eine genaue Wegbeschreibung:
Er zeigt, wie weit du in jede Richtung gehen musst, um von einem Punkt (Bsp. Koordinatenursprung) zu einem Punkt (Bsp. Punkt P) zu gelangen. Vektoren, die vom Koordinatenursprung zu einem Punkt zeigen, nennt man Ortsvektoren.
Das bedeutet:
a Schritte in x-Richtung
b Schritte in y-Richtung
c Schritte in z-Richtung
Probiere in dem folgenden Applet aus, den Punkt P mit den Schieberegler zu verschieben und ihn dann in einen Ortsvektor umzuwandeln!
Vektoren zwischen Punkten
Es ist zudem möglich, Vektoren von einen zu einen anderen Punkt zu berechnen.
Jetzt soll herausgefunden werden, wie man vom Punkt A zum Punkt B gelangt. Gesucht ist also der Vektor von A nach B, der dir genau beschreibt, wie du dich von A aus zu B bewegen musst. Gleiche Vektoren haben denselben Betrag (Länge) und dieselbe Richtung. Das bedeutet, sie verlaufen parallel zueinander und zeigen exakt in dieselbe Richtung – auch wenn sie an verschiedenen Punkten im Raum beginnen.
Vektoren mit gleicher Richtung haben denselben Richtungsverlauf (d. h. sie sind parallel), können sich aber in ihrer Länge unterscheiden.
Probiere auch das im folgenden Applet gerne aus!
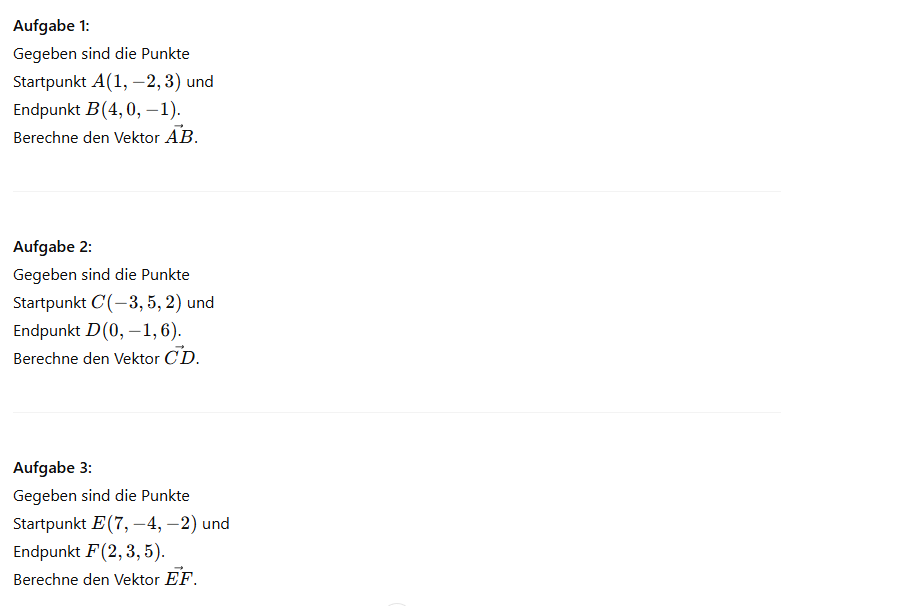
Einen Vektor vom Anfangspunkt A zum Endpunkt B rechnet man folgendermaßen aus:

Übung 1:
Entscheide welche Aussagen über die darunter stehenden Vektoren stimmen
Übung 2: Überprüfe deine Ergebnisse mit dem passenden Applet