1.2 ¿Qué es el Algebra Lineal?
Los dos problemas fundamentales del algebra lineal son: , sistema de ecuaciones , valores y vectores propios Si las matrices son cuadradas, el primer problema = tiene una única solución cuando las columnas de A son independientes. El segundo problema cuando tiene solución para y para produce vectores independientes (llamados vectores propios). Una parte importante de este curso es aprender el significado de "independencia". Lo mejor es aprender a partir de ejemplos. Se puede observar que:
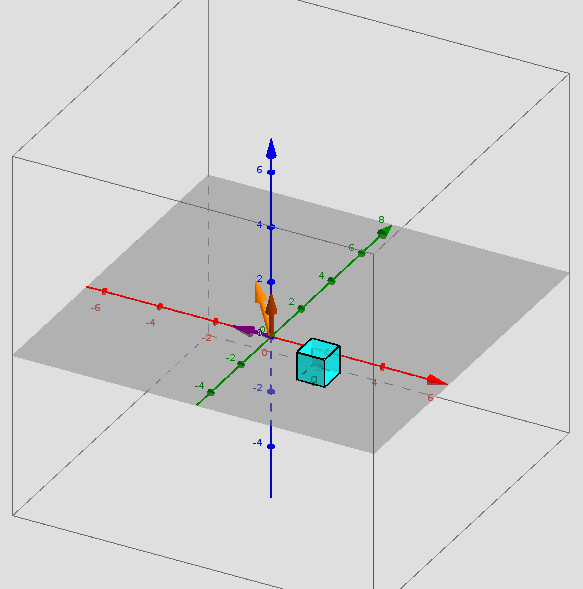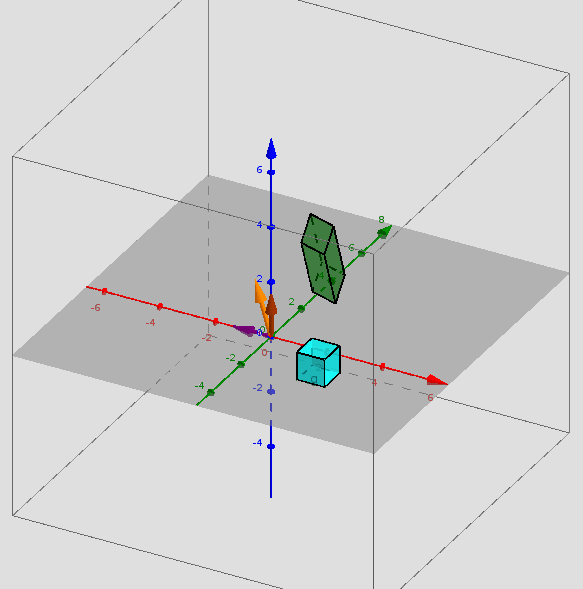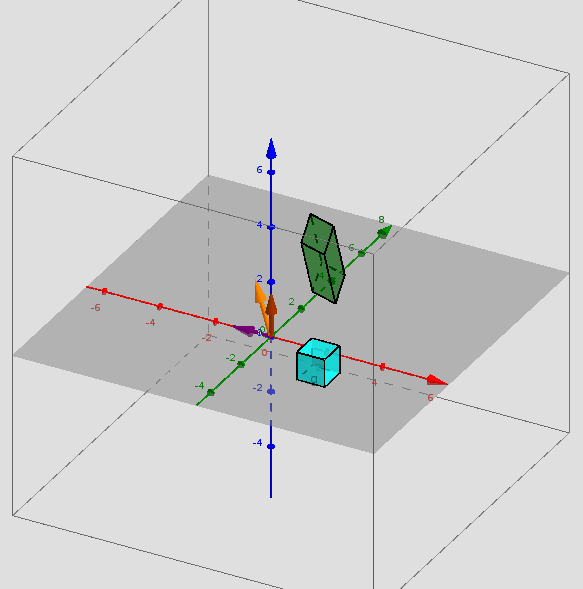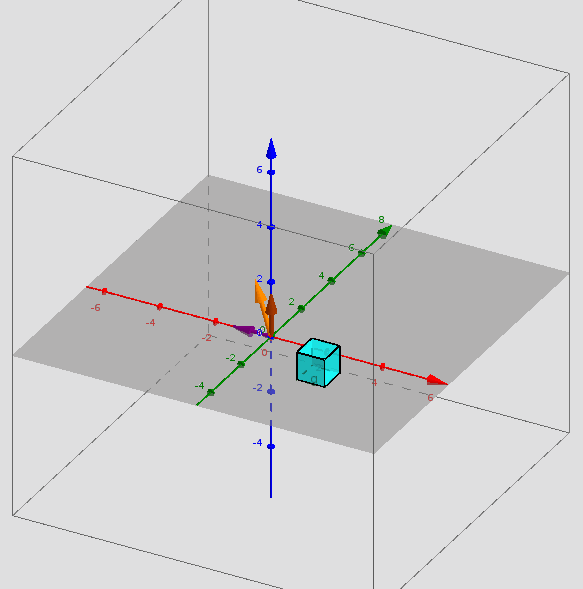
Si sumamos las columnas 1 y 2 obtenemos la columna 3. Un resultado sorprendente e importante del álgebra lineal establece que las filas tampoco son independientes. La tercera fila debe estar en el mismo plano que las dos primeras. Con alguna combinación de los renglones 1 y 2 se obtiene el renglón 3. Quizá el lector , en la siguiente actividad, pueda encontrar rápidamente esta combinación (yo no pude). Actividad: Intente mover los deslizadores c y d hasta que el vector naranja sea el vector , ¿Cuáles son los valores de c y d?Una matriz se puede ver como un conjunto de vectores, como en este caso, y esta visión es tremendamente útil en particular para entender el concepto de espacio vectorial que veremos más adelante.Otra manera de ver una matriz es por filas y est nos llevará a nuestro primer tema grueso del curso, el método de eliminación, un método general para resolver cualquier sistema de ecuaciones lineales. La eliminación es una forma simple y natural de convertir una matriz en otra "equivalente" que tiene bastantes elementos iguales a cero y está sera la clave para resolver el sistema de ecuaciones.Por tanto, el curso empieza aquí. ¡Pero no se quede demasiado ! El lector debe proceder de resolver sistemas de ecuaciones a construir combinaciones de las filas ylas columnas y analizar la independencia de estas y de ahí a las dimensiones de los espacios fila y columna. Este es el objetivo clave, abordar todos los espacios formados por los vectores: el espacio fila, el espacio columna y el espacio nulo. También es importante comprender la manera en que actúa una matriz sobre un vector. Cuando A (matriz) se multiplica por (vector) se obtiene un nuevo vector . Si el vector recorre todos sus posibles valores, todo el espacio de vectores se mueve; es "transformado" por A. Entender estas transformaciones nos da luz para entender diferentes clases de matrices que son esenciales en el estudio del álgebra lineales: matrices diagonales, matrices ortogonales, matrices triangulares y las más importantes las matrices simétricas. La belleza del álgebra lineal se puede apreciar de varias maneras: 1. Visualización. Combinación de vectores. Espacios de vectores. Rotación, reflexión y proyección de vectores. Vectores perpendiculares. Cuatro espacios fundamentales. 2. Abstracción. Independencia de vectores. Base y dimensión de un espacio vectorial. Transformaciones lineales. Descomposición del valor singular y la mejor base. 3. Cálculo. Eliminación para producir matrices que resuelven sistemas de ecuaciones. Gram-Schmidt para producir vectores ortogonales. Valores propios para resolver ecuaciones diferenciales y estabilidad de sistemas dinámicos El énfasis de este libro está en la comprensión: se intenta explicar, más que deducir. Es importante que el lector trabaje las diferentes actividades interactivas planteadas en el libro y no se conforme con su lectura de manera pasiva.Se ilustrarán ejemplos para enseñar lo que necesitan los estudiantes, de igual manera se brindarán referencias a videos y enlaces que reforzarán los conceptos del libro.
Este corto video sobre la enseñanza del Algebra Lineal del profesor del Mit Gilbert Strang , resume de excelente manera lo que acaba de leer, le puede interesar: