Ecuaciones exponenciales
Una ecuación exponencial es aquella que tiene expresiones exponenciales, es decir, potencias cuyos exponentes tienen en sus expresiones el factor desconocido x .
Por ejemplo:
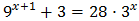
en este trabajo, resolveremos las ecuaciones exponenciales sin usar logaritmos. Este método de resolución consiste en alcanzar la igualdad de las exponenciales con la misma base para igualar los exponentes.
en este trabajo, resolveremos las ecuaciones exponenciales sin usar logaritmos. Este método de resolución consiste en alcanzar la igualdad de las exponenciales con la misma base para igualar los exponentes.
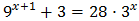
en este trabajo, resolveremos las ecuaciones exponenciales sin usar logaritmos. Este método de resolución consiste en alcanzar la igualdad de las exponenciales con la misma base para igualar los exponentes.
en este trabajo, resolveremos las ecuaciones exponenciales sin usar logaritmos. Este método de resolución consiste en alcanzar la igualdad de las exponenciales con la misma base para igualar los exponentes.1. Recuerda...
Antes de empezar, recordemos las propiedades de las potencias:
Producto
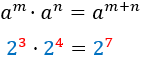
Cociente
Cociente
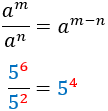
Inverso
Inverso
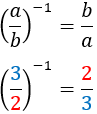
Potencia
Potencia
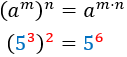
Exponente negativo
Exponente negativo
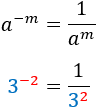
Inverso del inverso
Inverso del inverso
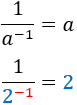
2. Ecuaciones resueltas
Equation 1
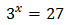
Teniendo en cuenta que , podemos reescribir la ecuación como
Teniendo en cuenta que , podemos reescribir la ecuación como
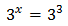
Por lo tanto, la solución es .
Por lo tanto, la solución es .
Ecuación 2
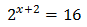
Teniendo en cuenta que , podemos reescribir la ecuación como
Teniendo en cuenta que , podemos reescribir la ecuación como
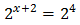
Entonces tenemos la ecuación lineal . Por lo tanto, la solución es .
Entonces tenemos la ecuación lineal . Por lo tanto, la solución es . Ecuación 3
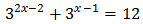
Teniendo en cuenta que
Teniendo en cuenta que
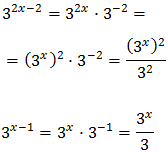
Podemos reescribir la ecuación como:
Podemos reescribir la ecuación como:
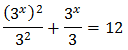
Tenemos la base común , pero como uno de ellos está al cuadrado, escribimos
Tenemos la base común , pero como uno de ellos está al cuadrado, escribimos
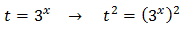
Sustituyendo, la ecuación termina como:
Sustituyendo, la ecuación termina como:
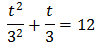
En otras palabras, una ecuación cuadrática:
En otras palabras, una ecuación cuadrática:
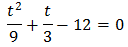 Multiplicamos la ecuación completa por 9:
Multiplicamos la ecuación completa por 9:
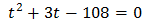
La resolvemos:
La resolvemos:
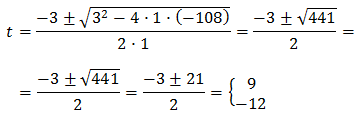
Por lo tanto,
Por lo tanto,
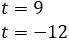 Entonces, obtenemos:
Entonces, obtenemos:
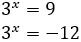
La segunda opción no es posible porque es negativa. Por lo tanto,
La segunda opción no es posible porque es negativa. Por lo tanto,
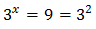
De donde obtenemos la única solución.
.
De donde obtenemos la única solución.
.

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.