moltiplicazione numero per punto
- Autore:
- Gae Spes
- Argomento:
- Moltiplicazione
Moltiplicazione di un numero reale (moltiplicatore) per un punto (moltiplicando).
Omotetia (ingrandimento o rimpicciolimento): B --> A∙B (di rapporto A).
Caso particolare in cui il moltiplicando B' è un numero reale.
operatori di moltiplicazione e omotetie
- moltiplicatore e moltiplicando: nell'espressione del prodotto x•z il primo fattore x è detto moltiplicatore (e in questo caso è reale) e il secondo fattore z è detto moltiplicando. Estenderemo successivamente la moltiplicazione al caso di moltiplicatore complesso
- operatori di omotetia (moltiplicatore fisso): se si fissa un numero reale x, la funzione da C a C definita dalla corrispondenza z
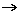x•z è detta omotetia di rapporto x. Ponendo Hx(z) = x•z, si ottiene la notazione Hx per tale omotetia. Come fatto con le traslazioni, possiamo far agire anche le omotetie su intere figure (vedi la figura qui a sinistra)
- composizione di omotetie: in maniera analoga a quanto accade per la composizione di traslazioni, l'omotetia composta Hx
Hy è tale che:
(HxHy)(z) = Hx(Hy(z)) = x(yz) = (xy)z = Hxy(z)
e pertanto risulta: HxHy = Hxy = Hyx
- valgono le seguenti proprietà delle omotetie: (sono dimostrabili facilmente: prova a dimostrarle)
- commutatività: dalla commutatività della moltiplicazione in R segue: HxHy = HyHx
- associatività: la composizione di funzioni è sempre associativa: (fg)h = f(gh). In particolare ciò, quindi, vale per le omotetie
- neutralità dell'omotetia identica: l'omotetia di rapporto unitario H1 è la funzione identità 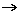zz
- invertibilità di un'omotetia non degenere: l'omotetia H0 è la funzione identicamente nulla z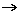0 ed è detta omotetia degenere. Se x non è nullo, Hx è detta non degenere; in tal caso l'omotetia inversa è H1/x , ossia:
Hx-1 = H1/x ( tieni presente che (1/x)xz = x(1/x)z = z, visto che x(1/x)=1 e viste la commutatività e l'associatività )
- linearità di un'omotetia: Hx(z+w) = Hx(z) + Hx(w) ( ricorda la proprietà distributiva del moltiplicatore )
e Hx(r·z) = r·Hx(z) (dove r
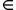R) ( tieni presente l'associatività dei moltiplicatori e la commutatività x·r = r·x ) .