Outline
Secuencias de Geogebra
Objetivo Secuencia de Exploración "Área y Perímetro del círculo" y OA asociado:
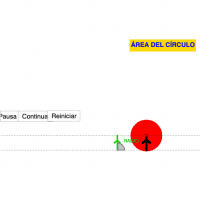
Objetivo: Explorar la relación entre diámetro y perímetro para deducir la constante π y la fórmula del perímetro, y luego descubrir la fórmula del área del círculo mediante la transformación del círculo en un triángulo, conectando lo concreto con lo simbólico.
MA07 OA11 Mostrar que comprenden el círculo:
> Describiendo las relaciones entre el radio, el diámetro y el perímetro del círculo.
Indicadores de logro:
- Calcula el cociente entre el perímetro y el diámetro en diferentes casos y concluye que el valor se aproxima a π.
- Deduce la fórmula del perímetro del círculo a partir de la relación descubierta entre el diámetro y el perímetro.
> Estimando de manera intuitiva el perímetro y el área de un círculo.
Indicadores de logro:
- Analiza cómo cambia el área del círculo al duplicar el radio, concluyendo que el cambio es proporcional al cuadrado del radio.
- Relaciona la base del triángulo con el perímetro del círculo y la altura con el radio.
- Formula la regla general para calcular el área del círculo a partir de las observaciones realizadas.
Objetivo Secuencia de Comprobación "Relación de áreas":
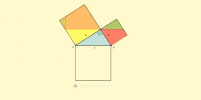
Objetivo: Comprobar la validez del teorema de Pitágoras mediante la exploración dinámica en un applet que muestra un triángulo rectángulo y los cuadrados construidos sobre sus lados, analizando la relación entre sus áreas y conectando representaciones concretas, pictóricas y simbólicas.
MA08 OA12 Explicar, de manera concreta, pictórica y simbólica, la validez del teorema de Pitágoras y aplicar a la resolución de problemas geométricos y de la vida cotidiana, de manera manual y/o con software educativo.
Indicadores de logro:
- Compara las áreas de los tres cuadrados y establece conjeturas sobre la relación entre ellas.
- Verifica si la relación se mantiene al modificar la forma del triángulo rectángulo, justificando con observaciones.
- Argumenta, a partir de la exploración, que el teorema de Pitágoras es aplicable a cualquier triángulo rectángulo.