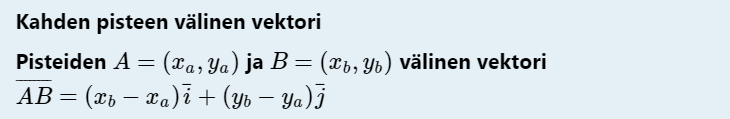Vektori xy -koordinaatistossa
Paikkavektori
"Kolme oikealle ja viisi ylös"
Koska vektorin voidaan ajatella kuvaavan tietyn suuruista siirtymää tiettyyn suuntaan, sen avulla voidaan antaa siirtymisohje origosta mihin tahansa paikkaan eli pisteeseen -tasossa. Origosta, eli pisteestä tiettyyn pisteeseen osoittavaa vektoria kutsutaan pisteen paikkavektoriksi. Kyseinen vektori kertoo meille reitin origosta paikkaan .
Siirtymiset -tasossa ilmoitetaan kantavektoreiden ja avulla
Siirtyminen -tasossa ilmoitetaan matkoina -akselin suuntaan ja -akselin suuntaan. Yhden yksikön mittaista siirtymää -akselin suunnassa kuvataan vektorilla ja yhden yksikön mittaista siirtymää -akselin suunnassa vektorilla .
Vektorit ja ovat koordinaattiakseleiden kanssa samansuuntaiset yksikkövektorit. Kantavektori osoittaa -akselin suuntaan ja kantavektori osoittaa -akselin suuntaan.
Esimerkki
| Kuinka origosta päästään pisteeseen vektoreiden ja avulla ja kuinka pitkä matka origosta on pisteeseen ? Ratkaisu: Oheisesta kuvasta nähdään, että pistettä vastaava paikkavektori on vektoreiden ja summa. Vektorin pituus saadaan laskettua pyhtagoraan lauseella: Vastaus: Siirtymä origosta pisteeseen vektoreiden ja avulla lausuttuna on ja etäisyys origosta pisteeseen on . | 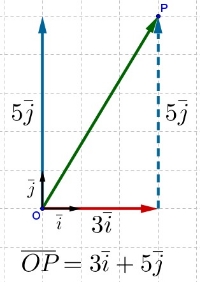 |

Pisteiden A ja B välinen vektori
Pisteiden ja välinen siirtymä, eli vektori voidaan esittää kantavektoreiden ja avulla. Piirretään tilanteesta kuva, johon merkitään origo , pisteitä ja vastaavat paikkavektorit ja , sekä vektori .
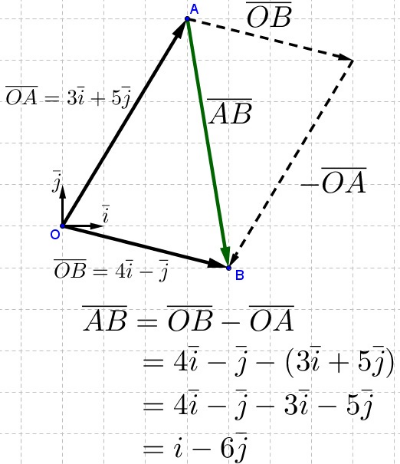
Kuvasta nähdään, että pisteestä päästään pisteeseen , kun siirrytään yksi oikealle ja kuusi alas. Samaan tulokseen päädytään myös laskemalla erotus Kahden pisteen välinen vektori muodostetaan aina vähentämällä loppupisteen paikkavektorista alkupisteen paikkavektori.