Graphs of Polynomials
THIRD-DEGREE POLYNOMIALS
The graph shows the polynomial . Investigate how the coefficients affect the shape of the graph.
TIP: How to effectively work with sliders.
Start by moving only the slider and observe how the graph changes. Then return its value back to 1.
Move the slider . What happens with the graph? When finished, set it back to 0.
Change the value of . Observe. Return to 0.
Move the slider .
Once you tried sliders individually, you can investigate what happens when you change more coefficients at the same time.
As you are changing the coefficients, the graph of a third-degree polynomial is also changing.
However, there are certain patterns that can be generalized for all third degree polynomials.
Use the applet to describe possible cases of graphs and answer the following questions.
Zeros (x-intercepts)
How many zeros can a third-degree polynomial have? Consider all possible cases.
Turning points and terrace points
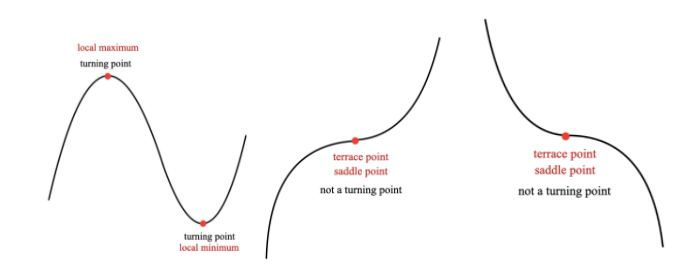
Turning points
What is the MAXIMUM NUMBER of turning points that a third-degree polynomial can have? (Turning point: local minimum or local maximum)
Terrace points
What is the MAXIMUM number of TERRACE POINTS that a third-degree polynomial can have?
FOURTH-DEGREE POLYNOMIALS
You will now be investigating graphs of fourth-degree polynomials.
Read the tip about working with the sliders.
Zeros
How many zeros can a fourth-degree polynomial have?
Turning points
What is the MAXIMUM NUMBER of turning points that a fourth-degree polynomial can have? (Turning point: local minimum or local maximum)
Terrace points
What is the MAXIMUM number of terrace points that a fourth-degree polynomial can have?
Higher-degree polynomials
The following applet allows you to analyze also some higher degree polynomials.
Your goal is to derive a general rule about the number of zeros and turning points of an n-th degree polynomial - see statements below.
GENERAL RULE about the number of ZEROS of a polynomial of n-th degree.
Complete the statement: Polynomials of degree have at most ......... real zeros.
GENERAL RULE about the number of TURNING POINTS of a polynomial of n-th degree.
Complete the statement. Polynomials of degree have at most ....... turning points.