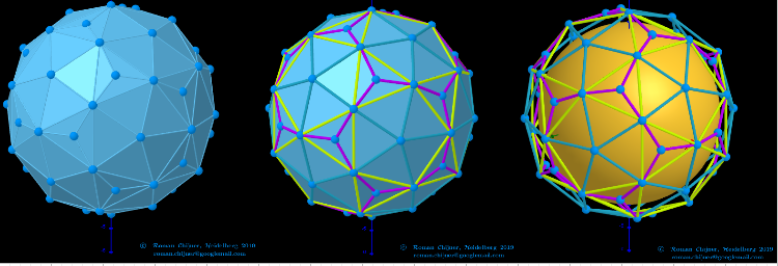
Images . Truncated icosidodecahedron (V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 4th-order segments
Generating Elements of mesh modeling the surfaces of polyhedron, its dual image and the coloring of their edges and faces can be found in the applet.
![[size=85]The elements of the Biscribed Pentakis Dodecahedron(4) -[b]Truncated icosidodecahedron[/b]. It bounded by:
[b]Vertices: [/b] V =120.
[b]Faces: [/b] F =62. 30{4}+20{6}+12{10}
[b]Edges: [/b] E =180. 60+60+60 - The order of the number of edges in this polyhedron are according to their length.[/size]](https://www.geogebra.org/resource/qa3sv5cg/ZFy2BlvrDUyfXcBz/material-qa3sv5cg.png)
Truncated icosidodecahedron:
https://en.wikipedia.org/wiki/Truncated_icosidodecahedron
| Type | Archimedean solid Uniform polyhedron |
| Elements | F = 62, E = 180, V = 120 (χ = 2) |
| Faces by sides | 30{4}+20{6}+12{10} |
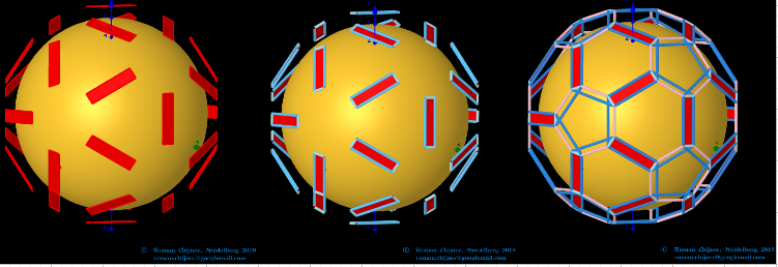

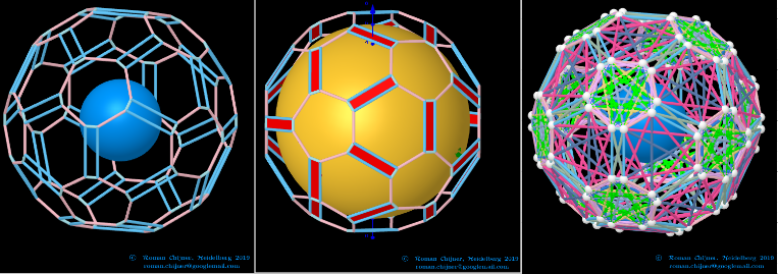
The elements of the dual to the Biscribed Pentakis Dodecahedron(4) (Truncated icosidodecahedron) -Disdyakis triacontahedron
Vertices: V = 62.
Faces: F =120. 120{3}
Edges: E =180. 60+60+60- the order of the number of edges in this polyhedron are according to their length.
| Disdyakis triacontahedron : |
| Type | Catalan |
| Conway notation | mD or dbD |
| Coxeter diagram | |
| Face polygon |  scalene triangle
scalene triangle |
| Faces | 120 |
| Edges | 180 |