กำเนิดพาราโบลา

บทนิยามของพาราโบลา

พาราโบลา (parabola) คือเซตของจุดทั้งหมดในระนาบซึ่งห่างจากจุดที่ตรึงอยู่กับ F ที่จุดหนึ่ง และเส้นตรง d ที่ตรึงอยู่กับที่เส้นหนึ่งเป็นระยะทางเท่ากัน จุดที่ตรึงอยู่กับที่นี้ เรียกว่า โฟกัส (focus) และเส้นตรงที่ตรึงอยู่กับที่นี้ เรียกว่า เส้นบังคับ หรือ ไดเรกตริกซ์ (directrix) ของพาราโบลา

พาราโบลา

คำชี้แจ้ง ให้นักเรียน 1. สร้างจุด C ซึ่งอยู่บนเส้นตรง d 2. สร้างส่วนของเส้นตรง CF 3. สร้างเส้นตรงแบ่งครึ่งและตั้งฉาก กับส่วนของเส้นตรง CF 4. สร้างเส้นตรง ที่ผ่านจุด C และตั้งฉากกับเส้นตรง d 5. สร้างจุดตัด ของเส้นที่คุณสร้างในข้อ 3 และข้อ 4 6. คลิกขวาที่จุดตัดในข้อ 5 และเลือก “แสดงรอย" (Trace On)

การสร้างพาราโบลาโดยนิยาม ด้วยโปรแกรม Geogebra

คำชี้แจ้ง ให้นักเรียน 1. เลื่อนแถบเลื่อน และเลื่อนจุด P 2. พิจารณาระยะห่างระหว่างจุด P กับ จุดโฟกัส และระยะห่างระหว่างจุด P กับไดเรกตริกซ์ 3. ศึกษาความสัมพันธ์ในข้อ 2 และตอบคำถาม

สำรวจพาราโบลา

พาราโบลา

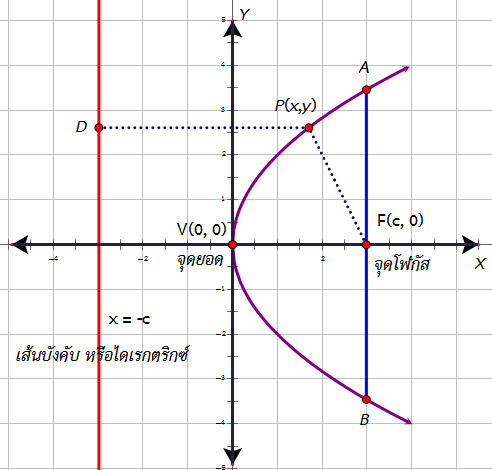
ส่วนประกอบของพาราโบลา

1. เส้นตรงคงที่เรียกว่า ไดเรกตริกซ์ ของพาราโบลา จากรูปคือ เส้นตรง

2. จุดคงที่เรียกว่า โฟกัส ของพาราโบลา จากรูปคือ จุด

3. เส้นตรงที่ผ่านโฟกัสและตั้งฉากกับไดเรกตริกซ์เรียกว่า แกนสมมาตร ของพาราโบลา จากรูปคือ แกน

4. จุดที่พาราโบลาตัดกับแกนของพาราโบลาเรียกว่า จุดยอด ของพาราโบลา จากรูปคือ จุด

5. ส่วนของเส้นตรงที่ตัดพาราโบลาโดยผ่านโฟกัสขนานกับไดเรกตริกซ์ และตั้งฉากกับแกนสมมาตร เรียกว่า เลตัสเรกตัม (latus rectum) จากรูปคือ ส่วนของเส้นตรง

จะได้ความยาวของเลตัสเรกตัมเท่ากับ

1.จากการสร้างพาราโบลาโดยนิยาม ด้วยโปรแกรม Geogebra จุดที่ได้จากการตัดกันของเส้นแบ่งครึ่งและเส้นตั้งฉากที่ผ่านจุด C คืออะไร

Marca todas las que correspondan