Parameter bei quadratischen Funktionen untersuchen
Aufgabe 1
Du kennst schon den Graphen der Funktion . Wenn du in deren Funktionsterm Faktoren oder Summanden änderst, verändert sich auch der dazugehörige Graph. Zum Beispiel zu .
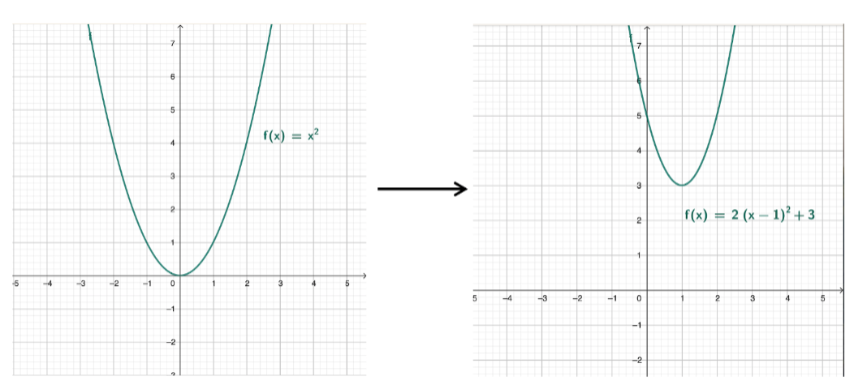
Wie hat sich der Graph von links nach rechts verändert? Beschreibe die Veränderung ganz genau.
Aufgabe 2
Wenn du im Funktionterm die Werte für den Faktor oder die Summanden oder änderst, so ändert sich auch der dazugehörige Graph. Untersuche nun mithilfe der Schieberegler in dem folgenden Funktionsplotter, wie sich der Graph der Funktion verändert.
Diese Schritte können hilfreich dabei sein:
- Betrachte zuerst Änderungen am Summanden . Nimm hierfür die Funktion und verändere die Werte von mithilfe des Schiebereglers.
- Betrachte anschließend Änderungen am Faktor . Nimm hierfür die Funktion und verändere die Werte von mithilfe des Schiebereglers.
- Betrachte dann Änderungen am Summanden . Nimm hierfür die Funktion und verändere die Werte von mithilfe des Schiebereglers.
Untersuche zunächst nur den Funktionsgraphen. Beobachte später auch, welchen Einfluss , und auf die Wertetabelle haben (Klicke auf "Wertetabelle anzeigen").
Aufgabe 3
Versuche nun, deine Erkenntnisse aus Aufgabe 2 zu begründen.
Die folgenden Schritte können hilfreich sein:
- Begründe den Einfluss von . Elise findet, dass der Graph im folgenden Bild enger wird durch den Parameter . Marcus sagt, dass die Form des Graphen unverändert bleibt. Wer hat recht? Versuche, das mit der Wertetabelle zu begründen.
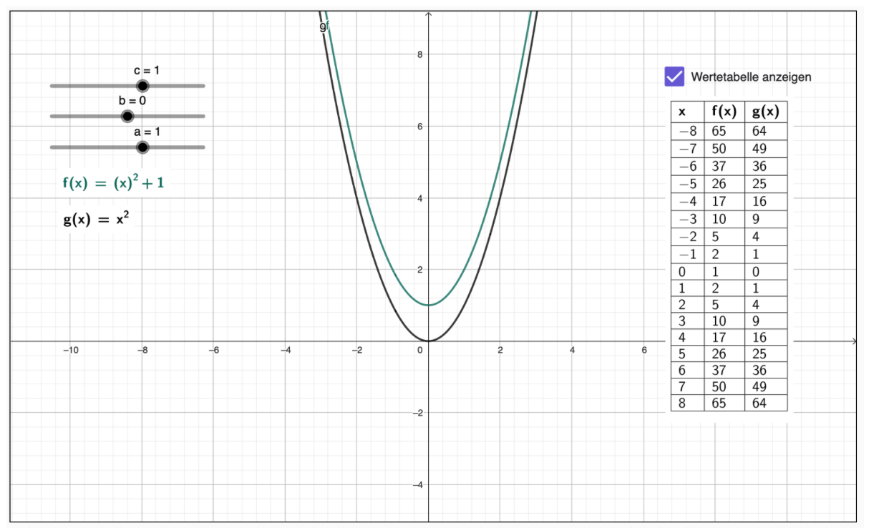
- Begründe den Einfluss von . Vergleiche dafür die erzeugten Graphen aus Aufgabe 2 und vergleiche sie mit der Normalparabel. Beschreibe genau, wie sich der Graph verändert und wieso. Betrachte dafür auch die Wertetabellen: Was ist z.B. der Unterschied zwischen und in den dazugehörigen Wertetabellen? Was ist die Ursache dafür?
- Begründe den Einfluss von . Schaue dir die Graphen der Funktionen und gleichzeitig an und vollziehe die folgenden richtigen Aussagen nach:
- "Wenn man sich statt anschaut, werden alle Werte in der Tabelle in Richtung größerer verschoben."
- "Für gilt , aber erst für gilt ."
Aufgabe 4
Erstelle ein Merkblatt mit allen Erkenntnissen, Ergebnissen und Begründungen aus den Aufgaben 1 bis 3.
Stell dir hierfür vor, du würdest einen Spickzettel für deine/-n Freund/-in schreiben, die in der heutigen Stunde nicht dabei war und eine Klassenarbeit über das Thema schreibt.
_______________________________________________________________________________________
Die Aufgaben stammen aus den Materialien von Lisa Göbel und Bärbel Barzel:
Göbel, L. & Barzel, B. (2021): Parameter digital entdecken - wirklich so easy? Mathematik lehren, 226, 20-24.
Göbel, L. (2021). Technology‑Assisted Guided Discovery to Support Learning: Investigating the Role of Parameters in Quadratic Functions (1 . Aufl.). Springer Spektrum Wiesbaden. https://doi.org/10.1007/978-3-658-32637-1