IM G Unit 1 Lesson 21
Here are 2 lines l and m that are not parallel that have been cut by a transversal.
Tyler thinks angle EBF is congruent to angle BCD because they are corresponding angles and a translation along the directed line segment from B to C would take one angle onto the other. Here are his reasons.
- The translation takes B onto C, so the image of B is C.
- The translation takes E somewhere on ray CB because it would need to be translated by a distance greater than BC to land on the other side of C.
- The image of F has to land somewhere on line m because translations take lines to parallel lines and line l is the only line parallel to l that goes through B'.
- The image of F, call it F', has to land on the right side of line BC or else line EF' wouldn’t be parallel to the directed line segment from B to C.
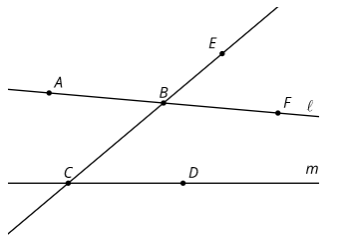
Pick one of Tyler's statement. Is the statement true? Explain your answer.
Pick one of Tyler's statement. Is the statement true? Explain your answer.
Here is triangle ABC with interior angles a, b, and c.
Points D and E are midpoints of sides AC and BC.
Draw line AB.
Use what you know about rotations to create a line parallel to line AB that goes through the opposite vertex.
Triangle Angle Sum One Way
What is the value of a + b + c? Explain your reasoning.
Triangle Angle Sum Another Way
Draw line AB.
Translate triangle ABC along the directed line segment from B to C to make triangle A'B'C'. Label the angles in triangle A'B'C'.
Translate triangle A'B'C' along the directed line segment from A' to C to make triangle A''B''C''. Label the angles in triangle A''B''C''.
Label the angles that meet at point C.
What is the value of a + b + c? Explain your reasoning.
IM G Unit 1 Lesson 21 from IM Geometry by Illustrative Mathematics, https://im.kendallhunt.com/HS/students/2/1/21/index.html. Licensed under the Creative Commons Attribution 4.0 license, https://creativecommons.org/licenses/by/4.0/.