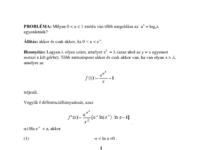
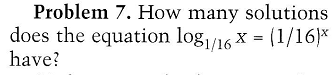Azonos alapú logaritmus és exponenciális ... (15.)
A közoktatás matematika anyagában szerepel az exponenciális és logaritmus függvény fogalma. Azt is megtanuljuk, hogy az azonos alapú exponenciális függvények és logaritmus függvények egymás inverzei.
KöMaL F. 2917.
Mekkora az és az függvények grafikonjainak távolsága, ha ?
Vizsgálódjunk a GeoGebrával!
Az látszik, hogy van olyan alap, amelynél a két grafikon metszi egymást. Ekkor a távolságuk 0.
A kérdés adódik:
Milyen a-ra van a két függvény grafikonjának közös pontja?
Először vizsgáljuk a függvényt! Milyen a-ra van a függvénynek zérushelye?
Az analízis eszközeivel meg lehet mutatni, hogy ha 1< a < , akkor a h függvénynek van zérushelye. Ekkor az f függvény grafikonja metszi az y = x egyenest. Az inverz függvények grafikonjai egymás tükörképei az említett egyenesre vonatkozóan, így az f és g függvények grafikonjai is metszik egymást, így a távolságuk 0.
A fent említett analízis eszközök
Ha nincs metszéspont
A keresett távolságot megkaphatjuk úgy, hogy megkeressük pl. az f függvény grafikonján azt a pontot, melyben az érintő pérhuzamos az y = x egyenletű egyenessel. A keresett távolság e pont és az x = y egyenes távolságának a kétszerese.
Az analízis eszközeivel kaphatjuk, hogy a keresett pont a , és a távolság .
A számolás a GeoGebrával:
És ha az alap kisebb, mint 1?
Az f szigorúan monoton csökkenő, folytonos függvény.
Az függvény szigorúan monoton növekvő és folytonos.
A fentiekből következik, hogy az f függvény grafikonja y = x egyenes metszi egymást a intervallumon.
Az inverz tulajdonság miatt ez a metszéspont illeszkedik a g grafikonjára is. Ez azt jelenti, hogy a két függvény grafikonjának legalább egy metszéspontja van. Az a kérdés követhet ezután, hogy lehet-e több metszéspont?
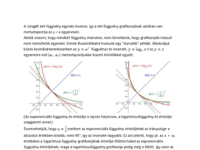
Ha az előző appletben kis a értékek esetén vizsgálódunk akkor gyanú ébredhet bennünk.
Itt jobban látható {f(x)/g(x)-1}
Az f és g grafikonjainak első koordinátai az függvény zérushelyei. Mint látható, e zérushelyek száma lehet 3 is és 1 is. Most már az a kérdés, hogy milyen alap esetén hány zérushely van. A problémát Dr. Németh József és Dr. Szilassi Lajos tanár urak is megoldották.
Dr. Németh József tanár úr bizonyítása
Dr. Szilassi Lajos tanár úr megoldása
A forrás: