Un Rompecabezas del teorema de Morley a partir de la demostración de John Conway

Frank Morley fue un matemático inglés que en 1887 se trasladó a EEUU para trabajar en el Haverford College (Pensilvania). En 1889 pasó a la Universidad Johns Hopkins, en Baltimore, institución en la cual permaneció durante 27 años hasta su retiro de la actividad docente e investigativa formal. En 1900 escribió el artículo “On the Metrics Geometry of the Plane n-lines”, publicado en la revista “American Mathematical Society Translations” y diversos autores reconocen que en el contenido de dicho documento se encuentra, de manera no explícita, el resultado conocido como “El teorema de Morley”. En su forma más simple esta proposición establece que: “Los puntos de intersección de las trisectrices interiores adyacentes de los ángulos de cualquier triángulo determinan un triángulo equilátero.” A partir de ese momento y durante más de 125 años se han publicado, y se siguen publicando, diferentes demostraciones de este resultado y artículos relacionados con el mismo; en particular en el año 2014, el profesor John Conway publicó en la revista The Mathematical Intelligencer, vol. 36, n. 3 el pequeño artículo On Morley’s Trisector Theorem, el cual contiene, por el momento, la demostración que se considera más sencilla del teorema de Morley. A grandes rasgos esta demostración consta de dos pasos básicos, a saber, a.      A partir de tres ángulos dados, cuya suma debe ser 60°, construir siete triángulos con características especiales, uno de los cuales debe ser equilátero. b.     Demostrar que estos triángulos se “acoplan” en un nuevo triángulo, semejante a uno dado cuyos ángulos son tres veces los ángulos conocidos. La siguiente gráfica ilustra el “encaje” de estos triángulos.

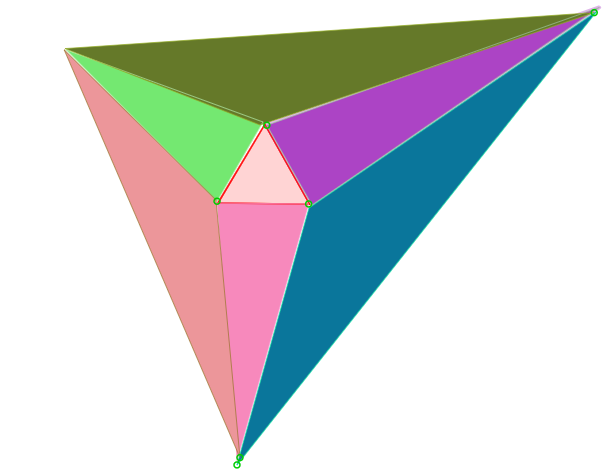
·        Al dar clic sobre, el botón “Nuevos ángulos”, se modifican los valores de los ángulos y consecuentemente el tamaño de los triángulos, así como su color. ·        Al activar la casilla “Teorema de Morley”, se muestra el enunciado de esta proposición. ·        Al activar la casilla “Instrucciones”, se muestra las indicaciones que permiten trasladar y rotar los triángulos. ·        Al activar la casilla “Puntos” se muestran los vértices del triángulo que debe acoplarse. La siguiente gráfica muestra los 7 triángulos “desacoplados”.