Lineare Optimierung grafisch (Script geführt)
Die Vorgaben strikt einhalten
Z: Zielfunktion
NB: Ungleichungen der Nebenbedingungen
- Button [ max ]/[ min ] ← Z entsprechend belegen
- Die Ungleichung sind in einer Liste {...} einzugeben {.... , .... , .... } Beginnt mit { Ungleichungen, mit, Kommata, trennen, schließt ab mit }
- NB(x,y) normalerweise: x>=0 && y>=0
- Mit dem Slider NBg (0,0)|0 können Sie die Eckpunkte des Lösungsgebietes abfragen und die Geraden-Gleichungen des Lösungsgebietes markieren
- Der Slider a kann als Variable in der Zielfunktion a x+ y oder in einer Nebenbedingung x + y <= a als interaktives Element eingesetzt werden um Veränderungen der Zielfunktion oder einer Nebenbedingung auf das Programm darzustellen.
- Falls a in den NB eingesezt wird sollte das Symbolic-Flag der Inputbox gesetzt sein, sonst erfolgt die Auswertung der NB-InputBox erst nach 2 mal Eingabe-Taste oder einer weiteren Änderung am LP.
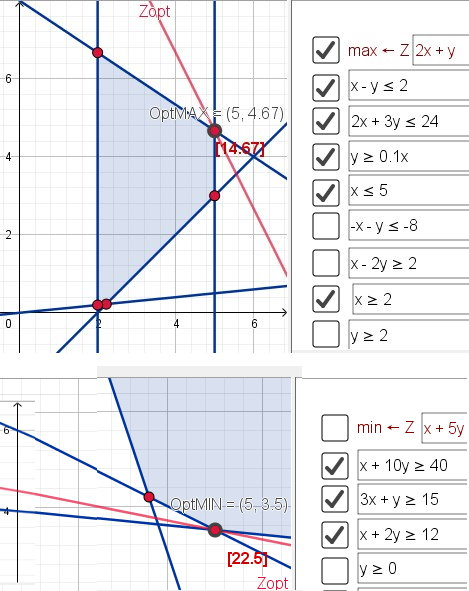
| 1.Max-Programm Max<= Z: 3x + 2y NB: y ≤ 0,5x + 4, y ≥ −2/5x + 2, y ≥ 0.1x 0,5 ≤ x ≤ 6 -App mit Anpassung NB -Link LP ohne Anpassung NB | 3.Min-Programm (zwingend erforderlich Anpassung) Min >= Z: x1+5x2 NB: 2x1 + 20x2 ≥ 80, 3x1 + x2 ≥ 15, x1 + 2x2 ≥ 12 x1>=0 ∧ x2>=0 |
| 2.Max-Programm Max<= Z: 2x+y NB(x,y):x>=2 ∧ y>=2 NB:{x - y <= 2 , 2 x +3 y <= 24 , y<=5 } | 3.Min-Programm Eingabe Min >= Z:x+5y NB(x,y):x>=0 ∧ y>=0 NB: x + 10y >=40 , 3 x + y >= 15 , x + 2y>=12 |
| Ein Bergbauunternehmen muß wöchentlich 1000 t Kohle der Qualität 1, 700 t der Qualität 2, 2000 t der Qualität 3 und 4500 t der Qualität 4 liefern. Die Kosten pro Schicht betragen bei Schacht A 40.000 EUR und bei Schacht B 100.000 EUR. | Die Förderung je Schicht ist folgender Tabelle zu entnehmen: Qualität 1 2 3 4 Schacht A 200 100 200 400 Schacht B 100 100 500 1500 40000*x+100000*y {200x + 100y = 1000, 100x + 100y = 700, 200x + 500y = 2000, 400x + 1500y = 4500} |
Ergebnis Beispiele 2 & 3 mit Link LP