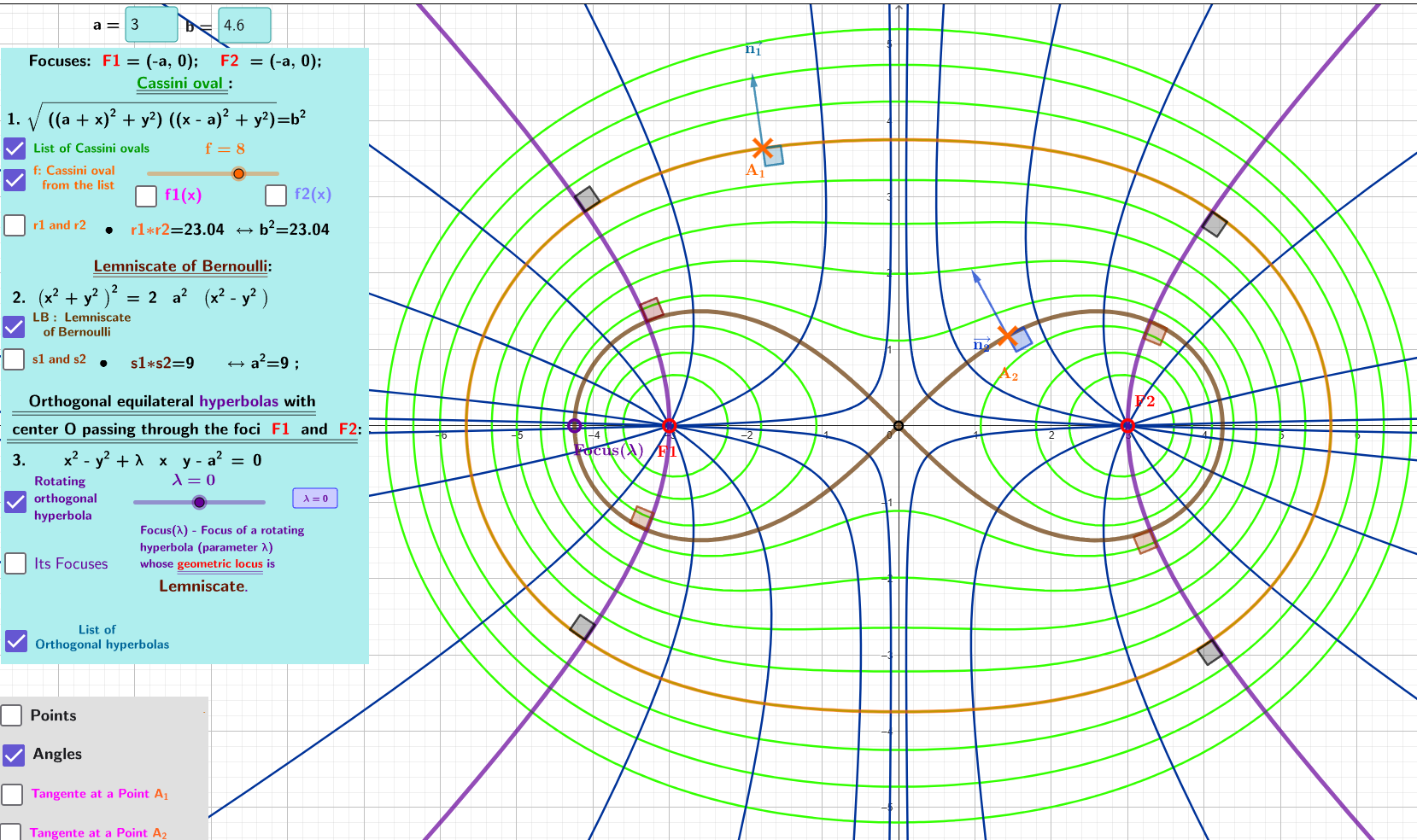
Cassini ovals and their orthogonal trajectories (hyperbolas)
The applet visualises the geometric properties of Cassini lines and their associated Bernoulli lemniscate - fourth-order curves that represent the locus of points such that the product of the distances of these lines to their two foci is constant.
1. The Lemniscate of Bernoulli is from the family of Cassini ovals where b=a.
2. For an arbitrary point A1 of the Cassini oval with foci: F1 and F2 the normal is the symmedian of the triangle △F1A1F2.
For an arbitrary point A2 of the lemniscate of Bernoulli with foci: F1 and F2 the normal is the symmedian of the triangle △F1A2F2.
3. The rectangular (or equilateral) hyperbolas: x² - y² + λ x y - a² =0 orthogonally intersect both the family of Cassini ovals and the Bernoulli lemniscate with the same foci: F1 and F2. Moreover, the locus of the foci of these hyperbolas is the lemniscate of Bernoulli.
Constructions