Water Tower Math

Author:
Brad Ballinger
Topic:
Circle, Geometry, Intersection, Line Segment, Multiplication, Secant Line or Secant, Tangent Line or Tangent
While hiking in the hills one day, I came across a wooden water tower--kind of like this one:
Image: www.watertanksales.com
Image: www.watertanksales.com
I wanted to estimate how many people it served, so I needed to figure out how big it was.
  • I could've measured the diameter if I got inside the tank. Not an option.
  • If the top was flat, I could've measured the diameter from up there. Didn't want to.
  • I could've paced out the circumference and divided by pi to find the diameter, but there were bushes growing too close around most of the tank.
I could walk up to the tank for maybe 1/3 of its circumference. How could I learn the diameter of the tank? As it happens, circles have an unexpected and useful property that most people don't know--a property that helped me answer the question. In this activity, we'll explore that property.

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

In the figure below, you can use the three blue points to determine a circle and place an observer. You can also use the green points to indicate lines of sight. The red points are there only for reference: you can't directly control those.

1. Mess around

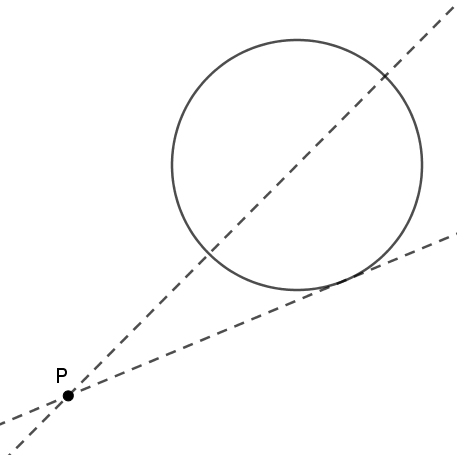
Move the five points that you can move. Your goal is just to get a sense of how they affect the diagram. Have you done that?

Select all that apply
  • A
Check my answer (3)

2. First observations

Use the reset button if you need to. Make the circle pretty big, and put point P somewhere inside it. As you move point A, do you notice any relationships between the two numbers along line segment AB?

Check my answer
Here's the same diagram with a little more information:

3. The Effect of Moving A or C

Leave the blue points where they are, but move A and/or C. What do you notice regarding the numbers in the new diagram?

Check my answer

4. The Effect of Moving P

Move P to a new location. What changes, and what stays the same? Explore with P inside, outside, or on the circle. (Can you make points A and B coincide?) (Notice that with P outside the circle, the two segments AP and BP overlap a little. One of the lines is dashed so that you can see both, even when they overlap.) Write some brief notes about what you discover.

Check my answer

5. Spoiler alert

Are you ready to see a summary of the pattern at play here?

Check my answer

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

It's time to find out how this helps us measure a water tower! Let's say I set down my pack at some point P near the water tower. I can measure the distance from my pack to the tower along two different lines. One way is to walk along a tangent line, so that my path just grazes the water tower. Another is to walk directly at the tower along the shortest possible path, which continues through the center of the circle and out the opposite side. The two lines are shown here:
Image

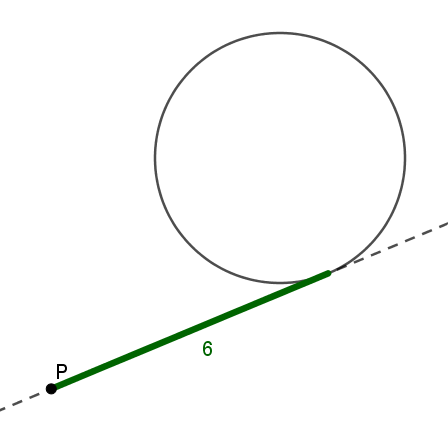
6. The product along one line

Suppose I walk along a tangent line. If it's 6 paces from my pack to the tower along this path, what is the value of the product, (near distance) times (far distance)? (See figure below.)

Check my answer

Figure: 6 paces to tower along a tangent line

Figure: 6 paces to tower along a tangent line

7. The product along another line

Now suppose it's only 4 paces from my backpack to the nearest part of the tower, as shown below. Since the (near)(far) product is the same as before, how far is it to the opposite side?

Check my answer
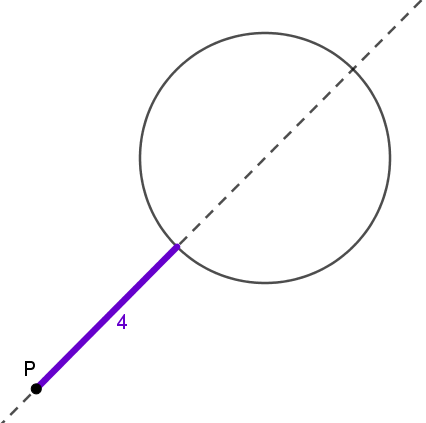
Image

8. Diameter

Using what you've figured out so far, what's the diameter of the tower?

Check my answer

New Resources

Discover Resources

Discover Topics