Einführung der Natürlichen Exponentialfunktion
Im Grafikrechner sind die Graphen der Funktion und die zugehörige Ableitung abgebildet. Der Graph der Ableitungsfunktion sieht dem der Funktion sehr ähnlich, es scheint also einen Zusammenhang zu geben.
Im Folgenden wollen wir überprüfen, ob die jeweiligen Funktionswerte an einer Stelle vielfache voneinander sind. Das würde bedeuten es existiert eine Zahl für die gilt: , also .
Aufgabe 1
Aufgabe 2
Im zweiten Grafikrechner sind die Funktionen sowie die Ableitungsfunktion zu sehen.
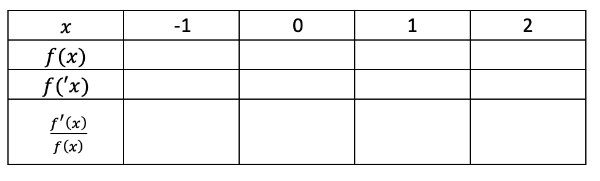
a) Ergänze die untenstehende Tabelle.
b) Vervollständige den Satz
"Die Funktion hat die Ableitung "
Aufgabe 3
Die Graphen der Ableitungsfunktionen aus Aufgabe 1 und Aufgabe 2 lagen überhalb bzw. unterhalb des Funktionsgraphen. Finde einen Wert a, sodass die Funktionen sowie die Funktion annähernd identisch sind.
Ergänze: Die Funktion mit a ≈ . . . . . ergibt abgeleitet sich selbst.