Transformationen UB
Verschieben und Strecken von Graphen
Schrittweise Transformationen ("Veränderungen") an Funktionsgraphen untersuchen.
Es gibt verschiedene Arten von Transformationen:
Verschieben von Graphen und Strecken/Stauchen von Graphen
Wir beginnen mit dem Verschieben von Graphen.
Lies dir zunächst einmal folgende Erklärungen durch:
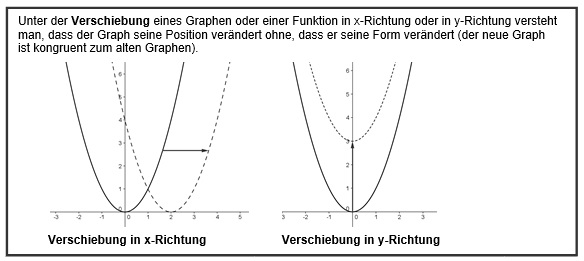
Einzelarbeit
Man kann einen Graphen sowohl in x- als auch in y-Richtung verschieben.
1. Verschiebung in y-Richtung
Einen Graphen in y-Richtung, d.h. "nach oben" bzw. "nach unten", verschieben kannst du bereits. Mithilfe der folgenden Graphen, die GeoGebra dir anzeigt, kannst du dies noch einmal wiederholen.
Arbeitsauftrag: Zeichne mithilfe von GeoGebra jeweils den um 2 nach oben und um 3 nach unten verschobenen Graphen (links im Eingabefenster eingeben und auf Enter drücken).
Formuliere eine passende Regel: Die Verschiebung eines Graphen in y-Richtung erreicht man, indem man die Funktionsvorschrift folgendermaßen abändert:
2. Verschiebung in x-Richtung
Einen Graphen in x-Richtung, d.h. "nach links" bzw. "nach rechts", verschieben kennst du ebenfalls bereits von Parabeln.
Arbeitsauftrag: Zeichne mithilfe von GeoGebra jeweils den um 2 nach rechts und um 2 nach links verschobenen Graphen (links im Eingabefenster eingeben und auf Enter drücken).
Partnerarbeit
Wie lässt sich dies nun auf andere Potenzfunktionen übertragen?
Verschiebtdie folgende Funktion um 2 Einheiten nach rechts.
Verschiebt sie anschließend um eine Einheit nach unten.
(Der Tipp unterhalb der beiden Funktionenfenster hilft dir, wenn du Hilfe brauchst.)
Verschiebt nun die folgende Funktion 2 Einheiten nach links und eine Einheit nach oben.
Tipp: Parabeln verschiebt man, indem man statt x z.B. (x-2) [Verschiebung um 2 nach rechts] oder (x+3) [Verschiebung um 3 nach links] schreibt. Ersetze das x in der Funktion ebenfalls durch eine Klammer +/- die Verschiebung.
Beschreibt in eigenen Worten wie ihr vorgegangen seid. Erläutert wie ihr die Funktionsvorschrift verändert habt.
Streckung (in y-Richtung)
a) Verändert den Streckungsfaktor a so, dass die Graphen jeweils durch den Punkt A verlaufen.
b) Verändert den Streckungsfaktor a so, dass die Graphen jeweils durch den Punkt B verlaufen.
Beschreibt erneut in eigenen Worten wie ihr vorgegangen seid. Erläutere insbesondere wie der Streckungsfaktor a den Verlauf der Funktion verändert.
Vertiefungsaufgabe (optional)
Verschiebe die Funktion eine Einheit nach links und 2 Einheiten nach oben. Wähle anschließend a so, dass die Funktion die y-Achse bei 3 schneidet.