Grafik Persamaan Garis Lurus
1. Pengertian Persamaan Garis Lurus
Perhatikan grafik dari fungsi dalam Koordinat Cartesius di bawah ini.
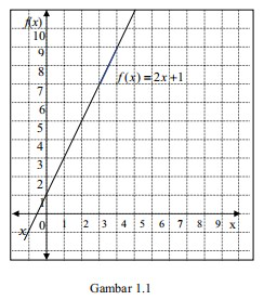
Sumbu mendatar disebut sumbu dan sumbu tegak disebut sumbu . Apabila fungsi di atas dituliskan dalam bentuk , maka sumbu tegak pada grafik disebut sumbu . Dengan Demikian .
Karena grafik dari fungsi atau berupa garis lurus, maka bentuk disebut persamaan garis lurus.
Bentuk umum persamaan garis lurus dapat dinyatakan dalam dua bentuk berikut ini.
a. Bentuk eksplisit
Bentuk umum persamaan garis lurus dapat dituliskan sebagai , dengan dan variabel atau peubah, dan konstanta. Bentuk persamaan tersebut dinamakan bentuk eksplisit. Dalam hal ini m sering dinamakan koefisien arah atau gradien dari garis lurus. Sehingga untuk garis yang persamaannya mempunyai gradien .
b. Bentuk implisit
Persamaan dapat diubah ke bentuk lain yaitu . Sehingga bentuk umum yang lain untuk persamaan garis lurus dapat ditulis sebagai , dengan dan peubah serta dan konstanta. Bentuk tersebut finamakan bentuk implisit.
Menggambar Grafik Persamaan Garis Lurus
Contoh 1.1
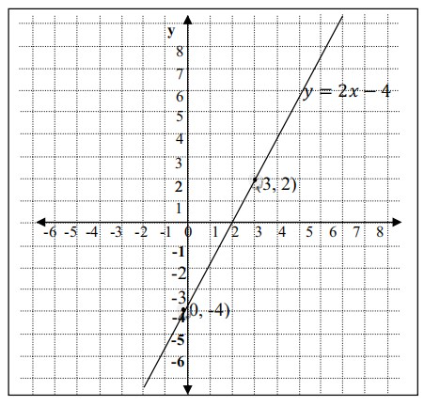
Gambarlah grafik persamaan garis lurus
Penyelesaian:
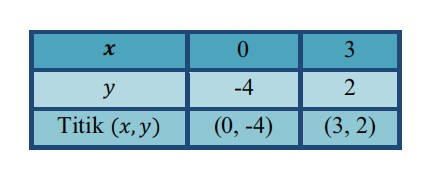
Persamaan
Jika , maka . Titiknya adalah
Jika , maka . Titiknya adalah
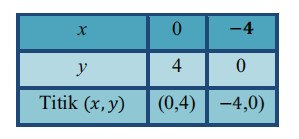
Tabel pasangan berurutan adalah:
Gambar grafiknya adalah sebagai berikut
Untuk mempermudah menggambar grafik persamaan garis lurus selain mencari dua titik sebarang yang memenuhi persamaan, dapat pula diambil dua titik yang merupakan titik potong grafik dengan sumbu dan titik potong dengan sumbu , sebagai berikut.
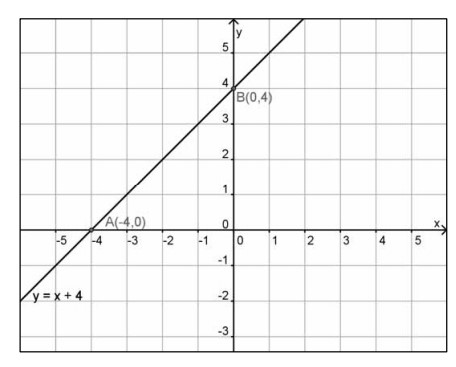
Gambarlah grafik persamaan garis lurus
Penyelesaian:
Persamaan
Titik potong dengan sumbu , yaitu jika , maka , titiknya adalah
Titik potong dengan sumbu , yaitu jika , maka , titiknya adalah
Tabel pasangan berurutannya adalah sebagai berikut:
Gambar Grafiknya adalah sebagai berikut: