Svelare il segreto dell'integrale definito: i teoremi
In questo capitolo ci occuperemo dei due teoremi che sono essenziali per capire le proprietà dell'integrale definito e della Funzione Integrale ad esso associata, e quindi per capire come calcolarli.
Iniziamo dal teorema della media, che partendo dall'ormai noto problema dl calcolo dell'area sottesa ad una funzione si pone l'obiettivo di riformulare il problema in termini più semplici e maneggevoli.
Notiamo che questo teorema introduce una condizione, che sarà richiesta ad ogni funzione affinché essa sia integrabile (cioè affinché sia possibile calcolarne l'area sottesa): la funzione deve essere continua. Il teorema della media infatti richiede che la funzione abbia una proprietà che abbiamo conosciuto esplorando i teoremi e le proprietà della funzioni continue, in particolare si appoggia sul teorema dei valori intermedi, che non a caso ha un nome simile.
Torneremo a questo aspetto, per il momento vediamo il contenuto e la dimostrazione del teorema in questa animazione.
Come sottolineato nell'animazione, la tesi può essere scomposta in due parti:
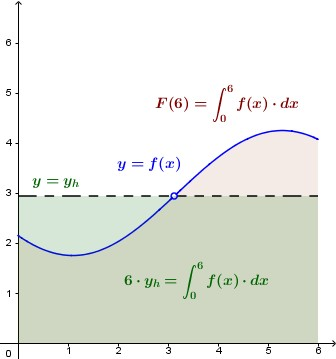
1) L'area sottesa alla funzione può essere espressa come superficie di un rettangolo che ha per base l'intervallo [a,b] considerato.
Questa parte è abbastanza evidente, perché qualsiasi numero può essere visto come prodotto di un numero arbitrario (la base fissata) ed un'opportuno altro numero (l'altezza che fa tornare i conti).
2) L'altezza può essere vista come output della funzione per un determinato valore compreso nell'intervallo di interesse .
Questa considerazione è meno semplice: richiede che esista un valore nell'intervallo per cui il risultato di per tale valore sia proprio . Questa richiesta è essenziale, perché permette di creare un legame tra l'area cercata e l'andamento della funzione , e ci fa capire che conoscendo la funzione potremo in qualche modo risalire al valore dell'area.
NOTA: la parte finale della dimostrazione si appoggia sul teorema dei valori intermedi; in realtà applica una combinazione di questo con il teorema di Weierstrass, quella spiegata al termine della pagina dei teoremi sulle funzioni continue.
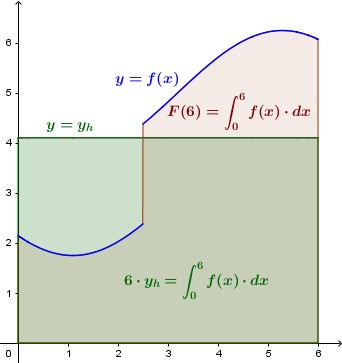
L'affermazione 2 è anche quella che non può essere data per scontata, come dimostrano i due controesempi riportati qui sotto.
CONTROESEMPIO 1
CONTROESEMPIO 2
IL TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE
Siamo pronti per trarre le nostre conclusioni sulla Funzione Integrale e sul calcolo delle aree sottese ai grafici, aggiungendo l'ultimo tassello che ci manca per capire questo meccanismo.
Dimostreremo che la Funzione Integrale è una delle primitive della funzione a cui si riferisce, e quindi per ottenerla sia sufficiente calcolare l'integrale indefinito di .
La dimostrazione di questa affermazione è il contenuto del Teorema Fondamentale del Calcolo Integrale, che la riformula verificando che la derivata della Funzione Integrale è proprio .
Vediamone l'impianto logico nella prossima animazione.
Il teorema ha dimostrato che se calcoliamo la derivata della Funzione Integrale e la valutiamo per un qualsiasi valore , otteniamo lo stesso risultato restituito dalla funzione di cui vogliamo calcolare l'area:
Dato che questo vale punto per punto in ogni , ne consegue che la derivata della Funzione Integrale coincide con la funzione di cui essa restituisce l'area sottesa.
Possiamo allora ricavare la relazione inversa: la Funzione Integrale è una delle primitive della corrispondente funzione .
![La relazione tra una funzione [math]f(x)[/math] e la sua Funzione Integrale [math]F(x)[/math]che permette di calcolarne l'area sottesa.](https://www.geogebra.org/resource/hpzcn54m/vBk1ajymncvpZDD3/material-hpzcn54m.png)
Abbiamo quindi che la Funzione Integrale è UNA delle primitive di :
Rimane un problema: QUALE primitiva deve essere considerata (cioè quale costante arbitraria ) per ottenere LA primitiva corretta che permette di calcolare l'area desiderata?
Vedremo fortunatamente che questo non è un problema per gli usi che faremo noi della Funzione Integrale.
IL CALCOLO DELL'AREA SOTTESA
Data una funzione , supponiamo di voler calcolare l'area sottesa al suo grafico nell'intervallo , in cui essa è continua.
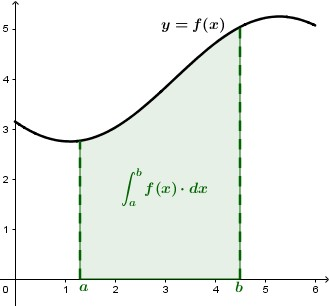
Tra tutte le primitive di , chiamiamo quella "giusta" che ci permette di effettuare il calcolo delle aree; è insomma la primitiva di , tra le sue infinite, per cui vale la definizione .
Per quanto abbiamo detto sulle proprietà della Funzione Integrale, ed in particolare per la proprietà che abbiamo identificato come 2a, sappiamo che l'area cercata può essere vista come la differenza tra gli output della funzione integrale agli estremi dell'intervallo:
Prendendo una primitiva a caso, che chiamiamo (è una lettera greca e si legge "fi"), in generale essa differirà dalla primitiva "giusta" per una costante , cioè avremo .
Verifichiamo ora calcolando l'analoga differenza con questa primitiva "sbagliata", , otteniamo comunque il risultato corretto, qualsiasi sia la primitiva che abbiamo scelto.
Per quanto abbiamo detto abbiamo che
analogamente abbiamo che
la differenza che ci proponiamo di utilizzare vale quindi
Risolvendo le parentesi scopriamo che si annullano le due costanti , e quindi otteniamo:
Abbiamo quindi ottenuto esattamente l'area cercata (vedi formula all'inizio della dimostrazione), e verificato che l'indeterminazione legata alla costante non influisce in questo calcolo, per il quale possiamo quindi utilizzare una qualsiasi delle primitive di .