Long division
- Author:
- P Porras
If the degree of a polynomial expression is more than 2 and at least one of the factors is
known, long division can be used to find the rest of the factors. The method is quite similar to long division for numbers.
Example 3. Divide 23456 by 123 with long division.
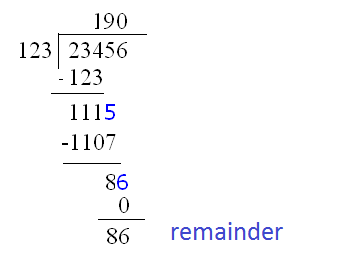
Example 4. Solve the division
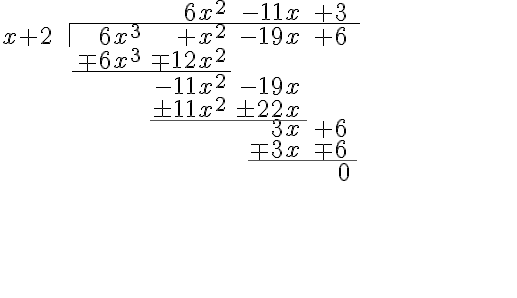
Example 5. Factorize
From previous example we know that
By finding the zeros for the quadratic expression, we can factorize the expression further