TRASLACIONES EN EL PLANO
En lenguaje matemático:
La traslación es una transformación puntual por la cual a todo punto A del plano le corresponde otro punto A' también del plano de forma que  .
Siendo
.
Siendo  el vector que define la traslación.
el vector que define la traslación.

Recordemos rápidamente qué es un VECTOR: Existen fuerzas en la naturaleza para las cuales son necesarias expresar por la cantidad (módulo), hacia donde se aplica (dirección) y desde-hacia donde se aplica (sentido). Se utiliza el concepto de vectores para representar este tipo de fuerzas. Un vector se representará por una flecha, en la cual irán implicitos su módulo (longitud de la flecha), dirección (inclinación de la flecha respecto de la horizontal) y sentido (la punta de flecha indica el punto final ).
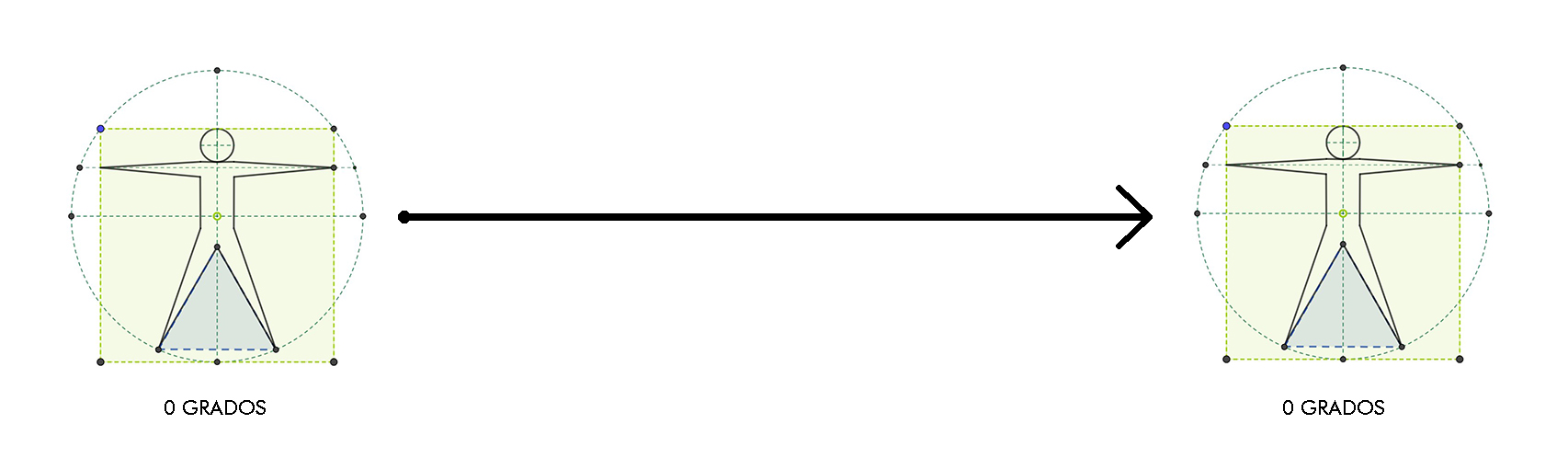
¿Se ha deformado Mario mientras lo trasladabas?
¿Qué le pasa al dibujo si cada punto del dibujo se traslada con un vector diferente
Vamos a terminar el capítulo introduciendo lo aprendido en la definición de traslación que dimos al principo:
Las traslaciones pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y tamaño de las figuras y objetos trasladados a las cuales deslizan según un vector.
Una traslación desplaza cada punto de una figura la misma cantidad en una misma dirección.
En geometría, una traslación es una isometría en el espacio euclídeo caracterizada:
por un vector →
