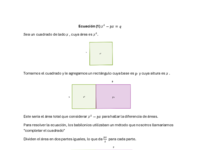
Ecuaciones cuadráticas en la antigüedad Babilonia
En la siguiente actividad se encontrarán ecuaciones cuadráticas con una variable, el reto presentado es resolverlas utilizando el método babilónico.
Tarea 1:
Dada la ecuación completar el cuadrado por medio de construcciones y razonamientos geométricos.
Recomendación: Utilizar el concepto de área del polígono geométrico cuadrado y rectángulo
Generalización de la ecuación cuadrática
Desde la época antigua y medieval e incluso a comienzos de la era moderna, las ecuaciones cuadráticas se clasificaron en tres tipos que reducimos a sus formas canónicas, son:
1.
2.
3.
Nos enfocaremos en la forma 1.
Pasos para la generalización de la ecuación :
Realice las siguiente construcción en la hoja de GeoGebra que aparece a continuación.
1. Construir un cuadrado de lado , cuya área será de .
2. Construir un rectángulo cuya altura es uno de los lados del cuadrado, de esta manera la altura es , la base de este rectángulo es .
3. El rectángulo de área , lo dividimos en dos partes iguales, de manera que el área de cada rectángulo será .
4. Construir un rectángulo de altura y base , esta base es uno de los lados del cuadrado inicial de área . Podemos afirmar que el área de este rectángulo es .
5. Ahora, supongamos que uno de los rectángulos que obtuvimos al hacer la partición en el paso 3, es el nuevo rectángulo que construimos. De esta manera tenemos un cuadrado. Es aquí donde surge lo que hoy en día conocemos como completar cuadrados.
¿Cuál es el lado del cuadrado mayor (cuadrado a completar)?
Continuando con la construcción:
6. Completando el cuadrado mayor, se añade un pequeño cuadrado de lado , cuya área es .
Podemos afirmar que el área total del cuadrado mayor es la suma de las áreas de los cuadriláteros contenidos en el: . De esta manera completamos el cuadrado con razonamiento geométrico de los antiguos Babilonios.
Ahora, de manera algebraica se demostrará cómo llegar a la fórmula cuadrática. Conociendo el lado del cuadrado podemos decir que: .
Por lo que ahora tendríamos:
Continuación demostración:
Finalmente,