Conic Sections with Polars
- Author:
- Kent Thele
- Topic:
- Cone, Conic Sections
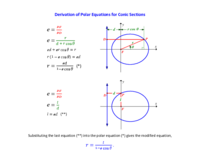
A common form for polar equations of conic sections is where is the eccentricity and is the distance from a directrix to its corresponding focus. This equation, unfortunately, cannot easily represent the simplest of all non-degenerate conics, the circle, because for circles: is zero and is infinite. However, replacing with another constant, , removes this limitation. The applet illustrates the modified form of the polar equation and connects the parameters of these equations to the conic-section namesake, the double-napped cone. A link to a file deriving these equations is also provided.
The applet shows a plane (in light green) intersecting a 45° double-napped cone. The cross section (in green) is projected onto the xy-plane, creating the conic section of interest (in blue). The projected conic section has a focus at the origin and a directrix at the intersection of the two planes. The polar equation given in the applet (where is the semilatus rectum and is the eccentricity) graphs the projected conic section. The applet will show that the size parameter in this equation, , is the z-intercept of the plane, and the shape parameter, , is the slope of the plane!
Kendig, Keith, Conics: The Dolciani Mathematical Expositions #29, MAA, 2005.
