Gauss-Algorithmus schrittweise JavaScript.GGB6.js
Beispiele
X = {{1, 1, -2, 3, 1}, {3, 4, 2, -3, 42}, {-1, 6, -7, 1, 50}, {-3, -2, 1, -2, -14}}
X = {{1, 3, 5, 7, 9, 11}, {0, 1, 3, 5, 7, 9}, {3, 5, 7, 9, 11, 13}, {1, 0, 2, 4, 6, 8}, {1, 4, 6, 8, 10, 12}}
1,2,3,4 ; 5,6,7,8 ; 6,4,3,10
-1,1,-1,1,2 ; 8,4,2,1,-1 ; -27,9,-3,1,44 ; 1,1,1,1,0
9,-7,7,-4,7,83 ; 6,8,5,1,-8,9 ; 0,-7,-1,-6,1,38 ; -2,-2,6,-7,9,-18 ; -9,-2,-7,0,5,-60
Beispiel mit abhängigen Gleichungen (Zeilen)
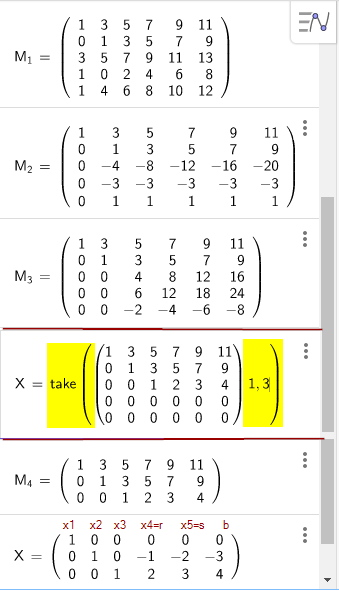
X={{1,3,5,7,9,11},{0,1,3,5,7,9},{3,5,7,9,11,13},{1,0,2,4,6,8},{1,4,6,8,10,12}}
Nach M3 entstehen in X Nullzeilen. Ich nehme die Nullzeilen weg, indem ich mit Take/Teilliste die Matrix auf die Zeilen 1-3 kürze (gelb unterlegte Ergänzung einschreiben oder 0-Zeilen löschen). Dann kann der Algorithmus weiter angewendet werden und als Parameterlösung x4=r, x5=s angegeben werden:
Gleichungssystem mit Parameter
1,3,-2,-7,3 ; 1,-5,-1,1,1 ; 1,-3,-1,6,-1
[Eingabe Matrix (click)]
[Gauss Schritt auf Matrix X ausführen]
...
x y z = a