緊張感のもとは単純?
ディミニッシュ7は単純だ
このワークシートはMath by Codeの一部です。
アプレット、背景、実装の順に見ていきましょう。

1.背景
1,3,5,7番目の音は
和音としても
ありふれた音の積み方、たし方ですね。
なにしろ、ドレミファソラシの音に音階にただ、奇数番目を押してできるからです。
そこで、偶数番目がスパイスになりそうです。2,4,6の音ですね。
ただ、7音を全部押しても音楽にはなりません。
そこで、単純なルールで「緊張感」のある和音を作ってみよう。
また、別の方法で、緊張感のある和音を作る方法を調べましょう。
<教会モードで度数の思い起こし>
C=1はイオニアン(メジャー)全全半全 全全半
D=1はドリアン 全半全全 全半全
E =1はフリジアン 半全全全 半全全
F =1はリディアン 全全全半 全全半
G=1はミクソ・リディアン 全全半全 全半全
A=1はエオリアン(マイナー)全半全全 半全全
B=1はロクリアン 半全全半 全全全
マイナーでもメジャーでも、
完全5度(全3半1)が大半なこと、
完全4度(全2半1)が大半なこと
この2つは変わりませんね。
3度は間の音程が2つありますが、半半はありませんでした。3度は全全か全1半1です。
全全というのは長3度(メジャー3)、全半か半全が短3度(マイナー3)です。
4和音にすることで、7度の音程に気づきました。半の音程は最高2つしかないので、
7度は全5半1か全4半2のどちらかです。
半1というのは長7度(メジャー7)、半2が短7度(マイナー7)ですが、
マイナー7が普通なのでマイナーをつけずにただの7度といいます。
つまり、5度、4度は基本的に完全が主ですが、3度と7度はメジャーとマイナーがあったのでした。
3度のマイナーはコードをマイナーにするのですが、
7度のマイナーはマイナー7なのに、ただの7をつけます。
マイナーでない7、つまりメジャー7はスケール上の7番なのに、レアなので逆にmaj7とか△7とか
かきましたね。
<偶数は7の上にある>
通常のコードでとばしてきた2,4,6は、響きの関係で飛ばすのが当然でしょう。
しかし、7の先にあるとして考えると、音のたし算ができるかもしれません。
2+7=9
4+7=11
6+7=13
つまり、7番コードの上に音をさらに重ねるのです。
すると、偶数に見えたものが、
7番を法とした剰余では偶数だったものが、
音階の主音から数えていくと、みな奇数番目ともいえるようになるのですね。
そうはいっても、音名でみると、一音違いの音を押させることになり、
とても緊張感があります。
7の上に積み重ねる和音をテンションコードといいます。
まぎらわしいですが、1音だけたし算する場合は別の言い方があります。
・sus4
11番ではなく4番として押すときはsus4とかsusとかいいます。
(例)
Gsus4 > G7のコード進行
・6番
13番ではなく6番として押すときは6番といいます。(例)C6。
<メジャースケール上の7和音>
白鍵の1番と3番と5番と7番の4和音の先に9番、11番、13番の3音を重ねた7和音を考えます。
1 3 5 78 9 11 13 15
C=1はイオニアン(メジャー)全全半全全全半|全|全半|全全|全半
D=1はドリアン 全半全全全半全|全|半全|全全|半全
E =1はフリジアン 半全全全半全全|半|全全|全半|全全
F =1はリディアン 全全全半全全半|全|全全|半全|全半
G=1はミクソ・リディアン 全全半全全半全|全|全半|全全|半全
A=1はエオリアン 全半全全半全全|全|半全|全半|全全
B=1はロクリアン 半全全半全全全|半|全全|半全|全全
1つとばしで、白鍵の奇数番号、1,3,5,7,9,11, 13を同時に引いたのが7和音です。
9番-8番が全だと、9度、半だとー9.
11番-8番が全全半だと11、全全全は+11
13番ー8番が全全半全全で13, 半が2つで-13
7和音を機械的にかくとどうなるでしょう。
C=1ではC3・7、 9, 11, 13。つまり、Cmaj7、9.11.13
D=1ではD-3・-7、9, 11, 13。つまり、Dm7、9.11.13
E=1ではE-3・-7、-9, 11, -13。つまり、Em7-9.11-13
F=1ではF3・7、 9,+11, 13。つまり、Fmaj7、9+11.13
G=1ではG3・-7, 9, 11, 13。つまり、G7、9.11.13
A=1ではA-3・-7,9, 11, -13。つまり、Am7、9.11-13
B=1ではB-3,-5,-7, -9, 11,-13。つまり、Bm7-5、-9.11-13
<メジャースケール上のテンションで避けたいもの>
4和音に対して、追加の3音がいつもたされるわけではありません。
テンションというより不安定、不協和な音程を避けることが必要です。
一般的には、次のように言われています。
・コードトーンの全全全差は避ける。
Dm7のー3とー13≡-6(mod7)は全全全の音程だから避ける。
・コードトーンと半音差は避ける。
9番
Em7のー9番のFは8番≡1番のEと半音差だから避ける。
Bm7-5のー9番のCは8番≡1番のCと半音差だから避ける。
11番
Cmaj7の11番≡4番のFは3番のEと半音差だから避ける。
G7の11番≡4番のCは3番のBと半音差だから避ける。
13番
Em7のー13番≡ー6番のCは5番のBと半音差だから避ける。
Am7のー13番≡ー6番のFは5番のEと半音差だから避ける。
7和音で、避けたいものを除いた残りは、
C=1ではCmaj7、9.13=C+Bm7(5ぬき)
D=1ではDm7、 9.11=Dm+C
E=1ではEm7、 11 =Em+D(3ぬき)
F=1ではFmaj7、 9+11.13=F+Emmaj7
G=1ではG7、 9.13=G+Fmaj7(5ぬき)
A=1ではAm7、 9.11=Am+G
B=1ではBm7-5、11-13=Bm-5+A7(3ぬき)
<一般化>
1番メジャースケール上のテンションコードは
1番maj7, 9. 13
2番m7、 9.11
3番m7、 11
4番maj7, 9+11.13
5番7、 9. 13
6番m7、 9. 11
7番m7-5、 11-13
<演奏上の注意>
全部のせということは少ないので、
7音コードを意識して、3和音+7番をベースにしたスケール上の4和音をつける
7,9,11,13⇒ ー6⇒ 7番を1とした1,3,5,7
テンションを強調するときは、3和音部分の3,5度は省いたりすることが多い。
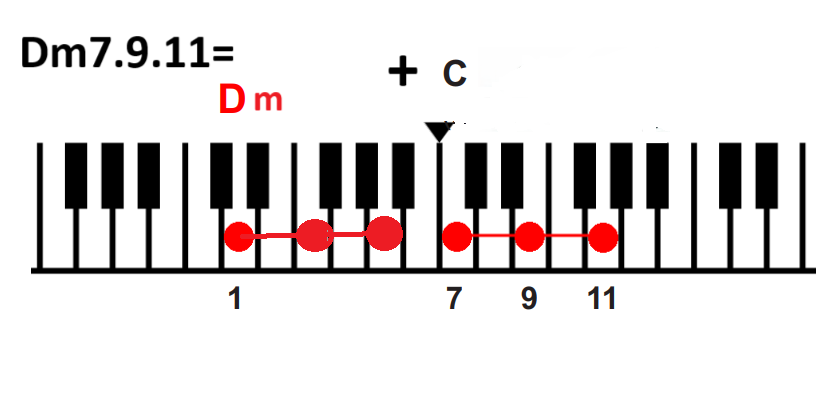
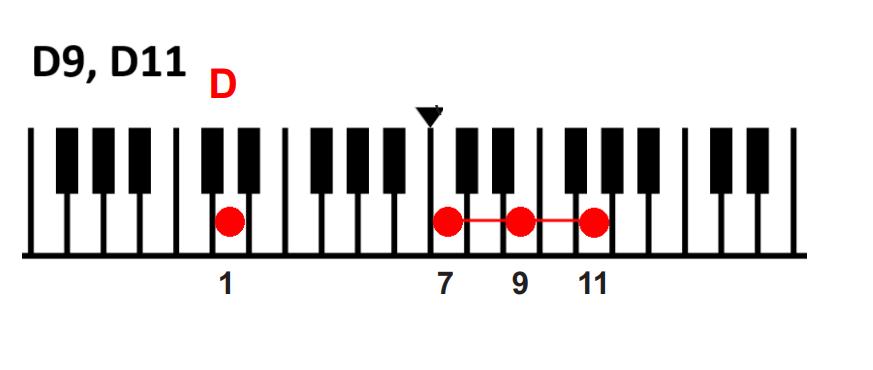
<ナチュラルマイナースケール上の7和音>
白鍵の1番と3番と5番と7番、9,11,13番を同時に押してみます。
1 3 5 78 9 11 13 15
A=1はエオリアン(メジャー)全半全全半全全|全|半全|全半|全全
B=1はロクリアン 半全全半全全全|半|全全|半全|全全
C=1はイオニアン(メジャー)全全半全全全半|全|全半|全全|全半
D=1はドリアン 全半全全全半全|全|半全|全全|半全
E =1はフリジアン 半全全全半全全|半|全全|全半|全全
F =1はリディアン 全全全半全全半|全|全全|半全|全半
G=1はミクソ・リディアン 全全半全全半全|全|全半|全全|半全
1つとばしで、白鍵の奇数番号、1,3,5,7,9,11, 13を同時に引いたのが7和音です。
7和音で、避けたいものを除いた残りは、
A=1ではAm7、 9.11
B=1ではBm7-5、11-13
C=1ではCmaj7、9.13
D=1ではDm7、 9.11
E=1ではEm7、 11
F=1ではFmaj7、 9+11.13
G=1ではG7、 9.13
<一般化>
1番ナチュラルマイナースケール上のテンションコードは
1番m7、 9. 11
2番m7-5、 11 -13
3番maj7、9. 13
4番m7、 9. 11
5番m7、 11
6番maj7、9+11.13
7番7、 9. 13
<ディミニッシュ>
ディミニッシュコードは名前も、説明も複雑に感じる人がいるかもしれません。
図形としてみると単純です。
たとえば、
Cメジャースケールでの7番目の4和音はBm7-5でした。
Bから白鍵だけを4つ押してB、D、F、Aです。
Bからみると1、-3、-5、-7というマイナスだらけです。
B=1はロクリアン |半全|全半|全全|全|
さて、ここで音程は12で1周したことを思い出してください。
そして、7度はメジャー7(全5半1)マイナー7(全4半2)の2種類が
スケールコードで生まれる7度でした。もう一声半音を増やした減7度(全3半3)を作るのです。
Bからみると1、-3、-5、ー-7というマイナスだらけです。
B=1でディミニシュ |半全|全半|全半|半全|
Bから順にB、D、F、G#の4つを押します。
さあ、これで、きれいに12個の半音階クロマチックスケールが4等分されました。
綺麗ですね。これをBdim7といいます。
BからみてG#が減7度(diminished 7th)だからです。
音程の均等性に目をつけると、
Bdim7=Ddim7=Fdim7=G#dim7になることがわかりますね。すべて半音あげると
Cdim7=D#dim7=F#dim7=Adim7です。さらに半音あげると
C#dim7=Edim7=Gdim7=A#dim7となります。今までのスケールの世界は、同型の和音はキーごとに12個できました。
ディミニッシュコードはキーを変えても、本質的に3個しかないことがわかりますね。
この事実を表したものが、最初のアプレットです。
2.実装
質問:ディミニッシュコードが視覚化できるアプレットはどうやって作りますか?
12種類の音名があるので、12角形の点にします。
たとえば、e^(i 2π/k) k=1...12として、12個の複素数z1からz12を設定しましょう。
12音名のリストNameS={"B", "C",......., "A#"}にたいして、
NameS(1), NameS(2),....,NameS(12)を1つ1つのテキストオブジェクトとして、
txt1, txt2,.....txt12と名前をつけなおします。
そうして、それぞれのテキストオブジェクトtxt kの「設定」の「位置」のリストから対応するzk
を選ぶべば、12個の頂点に、音名を表示できるようになるでしょう。
1つ1つの複素数の他に、複素数のリストpt=sequence(e^(i 2π/k), k, 1, 12)を設定しておけば、
pt(x)のxを適当に選ぶことで、スケールに関係のある点を強調できます。
(そして、選ばれた番号の頂点kに対して、mod(k-1,12)+1をすることで、12のときに12にする
変則mod12を作ることで、kの変化に対して、1,2、…、12、1,2、…。12と返します。)
選ばれたスケールの番号M={1,2,3,4,5,6,7,8,9,10,11,12}です。これがメジャーとの違いです。
キーをn=2としたばあい、M+n-1={2,3,4,5,6,7,8,9,10,11,12,13}と、リストをシフトして、MNという名前をつけます。そして、Sequence(Mod(MN(k)-1, 12)+1,k,1,12)として複素数の番号を12個に納めます。
たいていのスケールは7音ですが、クロマチックは12音なので、数列の範囲を7から12に変える必要があるので注意しましょう。
ここで、zip(pt(k),k,MN2)とするとMN2番目の頂点、つまりキーが2のスケール音名を強調できますね。
最後に和音がサイクリックな音名の関係、つまり円環構造なので、
スケール上の4和音の点を多角形の頂点として選びだしましょう。
4和音Cp4={MN2(i),MN2(i+3),MN2(i+6),MN2(i+9)}と番号リストを作ります。
すると、12等分の点からpolygon(pt(Cp4(1)),pt(Cp4(2)),pt(Cp4(3)),pt(Cp4(4))とするだけで四角形が指定できます。
くわしくは、かくれた「数式」を広げて、グラフィックビューを一時的にせまくして、観察しましょう。