"No Bending, No stretching"
1.7 No Bending or StretchingUNIT 1 • LESSON 7 NO BENDING OR STRETCHING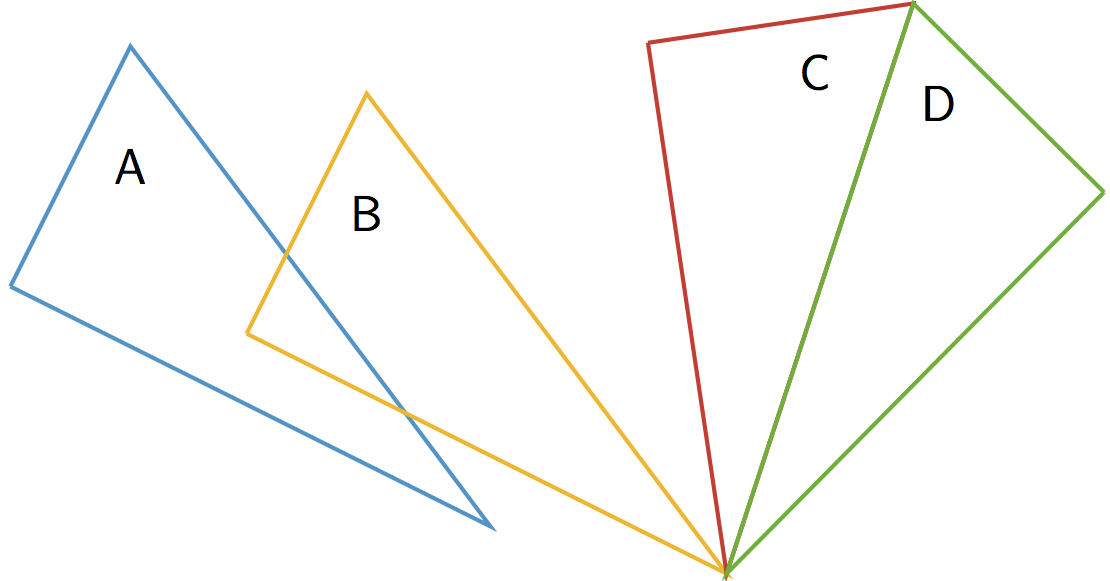 FAMILY MATERIALS:To review or build a deeper understanding of the math concepts, skills, and practices in this lesson, visit the Family Materials provided by Illustrative Mathematics Open-Up Resources. (Links to an external site.)Links to an external site.
FAMILY MATERIALS:To review or build a deeper understanding of the math concepts, skills, and practices in this lesson, visit the Family Materials provided by Illustrative Mathematics Open-Up Resources. (Links to an external site.)Links to an external site.
- Setting the Stage
- 7.1: Measuring Segments
- 7.2: Sides and Angles
- 7.3: Which One?
- Are You Ready For More?
- Summary
- Introduce the term rigid transformations.
- Observe that rigid transformations preserve lengths and angle measures.
- Demonstrating that I can describe the effects of a rigid transformation on the lengths and angles in a polygon.
 FAMILY MATERIALS:To review or build a deeper understanding of the math concepts, skills, and practices in this lesson, visit the Family Materials provided by Illustrative Mathematics Open-Up Resources. (Links to an external site.)Links to an external site.
FAMILY MATERIALS:To review or build a deeper understanding of the math concepts, skills, and practices in this lesson, visit the Family Materials provided by Illustrative Mathematics Open-Up Resources. (Links to an external site.)Links to an external site.