[고등수학탐구교실]줄리아 집합
유계인 궤도
복소다항식 에 대하여 과 같이 정의되는 수열 이 있다.
모든 자연수 에 대하여
인 실수 가 존재할 때, 의 궤도는 유계(bounded)라고 한다.
예를 들어, 에 대하여 의 궤도는 이므로 유계이다.
한편 의 궤도는 이므로 의 궤도는 유계가 아니다.
이와 같이 하나의 다항식에 대하여 첫째항에 따라 그 수의 궤도는 다양하게 나타난다.
복소다항식 에 대하여 의 궤도는 유계인지 아닌지 설명해보자.
채워진 줄리아 집합
복소다항식 에 대하여 채워진 줄리아 집합(filled-in Julia set) 는
로 정의된다.
예를 들어, 에 대하여 , , 이다.
줄리아 집합(Julia set) 는 채워진 줄리아 집합 의 경계(boundary)를 의미한다. 즉 줄리아 집합은 복소다항식 에 대하여 의 궤도가 유계인 점들과 유계가 아닌 점들의 경계이다.
판정법
복소다항식 에 대하여 라고 하자. 어떤 자연수 에 대하여 이면 이고 따라서 이다.
탈출 시간 알고리즘
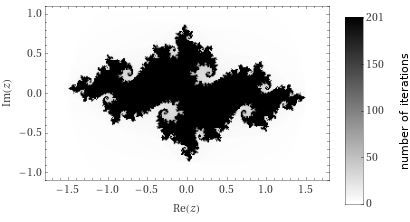
- 이면 를 만족시키는 를 구한다. 즉 이면 이다.
- 양의 정수 을 하나 선택한다. 이 양의 정수 은 각각의 복소수 의 궤도를 계산하는 횟수를 결정한다. 따라서 이 수가 크면 프로그램의 수행 속도는 느려진다.
- 색칠할 영역 을 선택한다. 채워진 줄리아 집합 의 전체 그림을 얻기 위해서는 영역이 반지름의 길이가 인 원을 포함해야 한다.
- 서로 다른 색 을 선택하는데 일반적으로 는 검은색으로 정한다. 여기에 선택된 점들은 영역의 특정 픽셀의 색을 정하는데 사용된다.
- 영역에 있는 한 점 을 잡아 이면 점의 색을 로 표시하고, 이고, 이면 점의 색을 으로 하며, , 인데 이면 점의 색을 로 표시한다. 이 과정을 계속하여 인 모든 정수 에 대하여 을 표시한다. 이때까지 표시되지 않은 점은 , 즉 검은색으로 표시하면 에 속하는 점은 모두 검은색으로 채색되어 줄리아 집합을 얻을 수 있다. 편의상 을 모두 흰색으로 표시하고 를 검은색으로 표시하면 에 속하는 점은 모두 검은색으로 채색되어 채워진 줄리아 집합을 얻을 수 있다.
지오지브라로 채워진 줄리아 집합 나타내기
지오지브라를 이용하여 위의 알고리즘에 따라 채워진 줄리아 집합을 나타내어보자. 이번 활동은 웹 지오지브라를 이용하지 않고, 지오지브라 클래식5를 이용하자.
- 입력창에 다음과 같이 입력하여 줄리아 집합을 결정하는 복소수 를 만든다. c=-0.74+0.11i 의 값은 임의로 입력한다.
- 입력창에 다음과 같이 입력하여 복소함수 를 만든다. f(x)=x^2+c
- 입력창에 다음과 같이 입력하여 탈출을 판단하는 수 를 만든다. R=(1+sqrt(1+4abs(c)))/2
- 색칠할 영역을 만들기 위해 입력창에 다음과 같이 입력하여 수 D를 만든다. D=ceil(10R)/10
- 슬라이더
도구를 이용하여 최솟값 0, 최댓값 (40D+1)^2-1, 증가 1, 속도 1/20인 수 t를 만든다. - 입력창에 다음과 같이 입력하여 함수 g(x), h(x)를 만든다. g(x)=-D+0.05(x-(40D+1)floor(x/(40D+1))) h(x)=-D+0.05floor(x/(40D+1)) g(x), h(x)는 보이지 않게 설정한다.
- 스프레드시트창의 A1셀에 다음과 같이 입력하여 영역 D를 움직이는 점을 만든다. =g(t)+h(t)i
- 스프레드시트창의 A2셀에 다음과 같이 입력한다. =f(A1)
- 스프레드시트창의 B1셀에 다음과 같이 입력한다. =조건(abs(A1)<=R,1,0)
- 스프레드시트창의 A2셀의 오른쪽 아래를 끌어내려 A30셀까지 자동채우기를 한다.
- 스프레드시트창의 B1셀의 오른쪽 아래를 끌어내려 B30셀까지 자동채우기를 한다.
- 스프레드시트창의 A2:A30 배열을 선택한 후, 마우스 우클릭하여 나타나는 메뉴에서 대상 보이기를 해제한다.
- 스프레드시트창의 A1셀의 설정사항-[고급 기능]-[동적 색상]의 빨강, 녹색, 파랑에 다음과 같이 입력한다. 빨강: 1-합(B1:B30)/30 녹색: 조건(곱(B1:B30)==1,0,1-합(B1:B30)/30) 파랑: 조건(곱(B1:B30)==1,0,1)
- 점 A1을 우클릭하여 나타나는 메뉴에서 자취 보이기를 활성화한다.
- 슬라이더 t를 우클릭하여 나타나는 메뉴에서 애니메이션 시작을 선택하여 채워진 줄리아 집합을 관찰한다.
역방향 반복 알고리즘
줄리아 집합을 만드는 다른 방법으로 귀납적 정의를 역방향으로 반복하여 이용하는 방법이 있다. 에서 이므로 제곱근을 선택하되, 개씩 항을 계속 구하여 이를 이용하여 계산하게 되면 항이 기하급수적으로 늘어나므로 두 제곱근 중 임의로 하나씩 선택하여 줄리아 집합을 나타낸다. 아래 그림은 울프럼알파에서 얻은 이미지(inverse iteration image)이다.
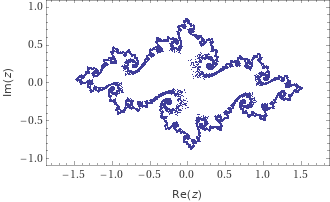
지오지브라로 역방향 반복 알고리즘 구현하기
지오지브라를 이용하여 위의 알고리즘에 따라 줄리아 집합을 나타내어보자. 이번 활동 역시 지오지브라 클래식5를 이용하자.
- 입력창에 다음과 같이 입력하여 복소수 를 만든다. c=-0.74+0.11i 의 값은 임의로 입력한다.
- 입력창에 다음과 같이 입력하여 복소함수 를 만든다. f(x)=x^2+c
- 입력창에 다음과 같이 입력하여 복소수 을 만든다. z_1=0i 이 복소수를 우클릭하여 나타나는 메뉴에서 자취 보이기를 활성화한다.
- 입력창에 다음과 같이 입력하여 반복횟수를 의미하는 변수 N을 만든다. N=0
- 버튼
도구를 선택한 후, 기하창에 버튼을 만들 위치를 클릭하면 나타나는 대화상자에 다음과 같이 입력한다.
캡션: 반복하기
스크립트
1 값설정(z_1,(-1)^랜덤(0,1) sqrt(z_1-c))
2 값설정(N,N+1) - 슬라이더 도구를 선택한 후, 기하창의 적당한 곳을 클릭하여 슬라이더 a를 만든다.
※ 최솟값, 최댓값, 증가 등은 수정하지 않아도 된다.
- 슬라이더 a의 설정사항-[스크립트]-[새로고침할 때]에 다음과 같이 입력한다. 마우스클릭실행스크립트(버튼1)
- 버튼
도구를 선택한 후, 기하창에 버튼을 만들 위치를 클릭하면 나타나는 대화상자에 다음과 같이 입력한다.
캡션: 그리기 시작
스크립트
1 애니메이션시작(a,true)
- 버튼 도구를 선택한 후, 기하창에 버튼을 만들 위치를 클릭하면 나타나는 대화상자에 다음과 같이 입력한다.
캡션: 그리기 중지
스크립트
1 애니메이션시작(a,false)
- 버튼 도구를 선택한 후, 기하창에 버튼을 만들 위치를 클릭하면 나타나는 대화상자에 다음과 같이 입력한다.
캡션: 초기화
스크립트
1 애니메이션시작(a,false)
2 화면이동(0,0)
3 값설정(z_1,0i)
4 값설정(N,0)
Julia Set
아래 바로가기를 눌러 다양한 c에 대한 줄리아 집합을 살펴보자.
Julia Set 탐구 사이트 바로가기