Outline
Searching for Eulerian and Hamiltonian Paths
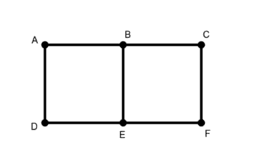
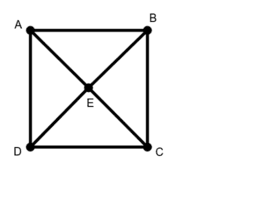
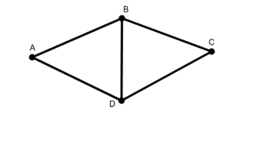
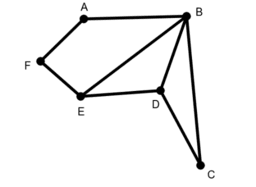
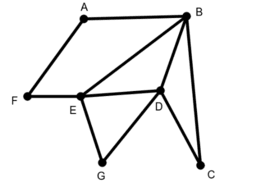
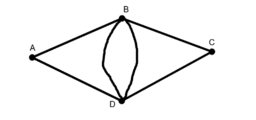
Study each of the 6 graphs provided.
(a) For each graph, find a Eulerian Path if one exists (i.e., a path for which each edge can be traversed exactly one time).
(b) Next, find a Hamiltonian Path if one exists (i.e., a path that visits each vertex exactly once).
(c) What do you notice about Graphs 4 and 5?
(d) What do you notice about Graphs 3 and 6?