ROTACIONES EN EL PLANO
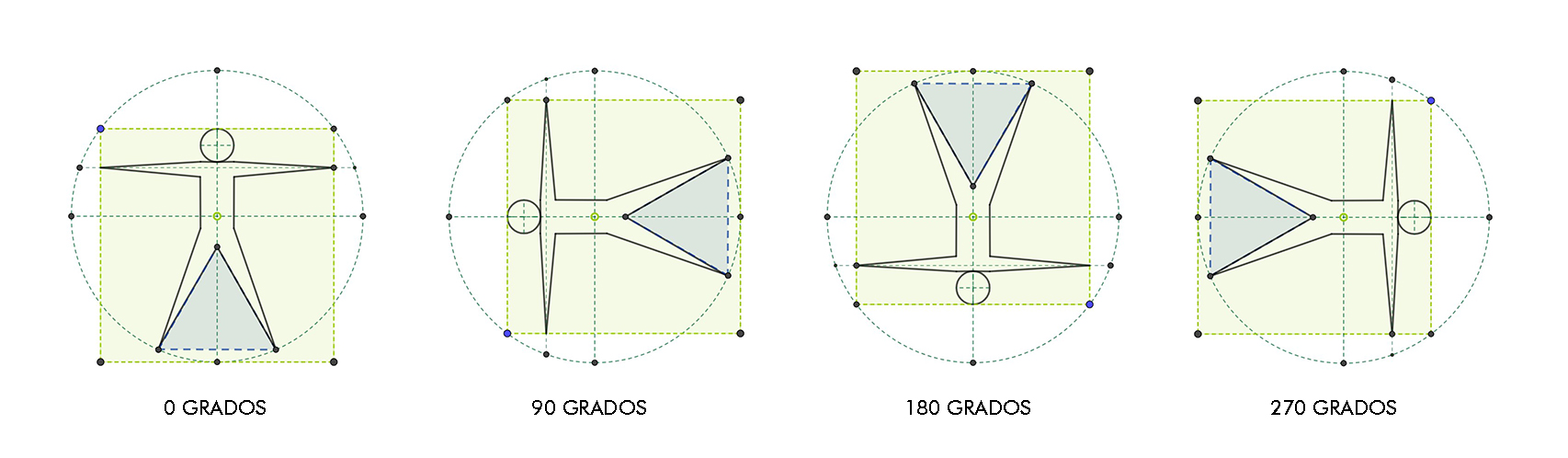
En matemáticas, la rotación es un concepto que tiene su origen en la geometría. Cualquier rotación es un movimiento definido en un determinado espacio donde el objeto conserva al menos un punto en su posición original.1 Puede describir, por ejemplo, el giro de un cuerpo rígido alrededor de un punto fijo. Una rotación es diferente a otros tipos de movimientos (como la TRASLACIÓN que no tiene puntos fijos; o la SIMETRIA). En siguiente ejemplo verás la ROTACION de la figura del HOMBRE de VITRUVIO que ya conoces. En este caso el eje de rotación ( es decir, el punto de su posición inicial que no cambia es el ombligo.
ACTIVIDAD 1 : Recordemos como medir ángulos en un plano con la ayuda de un transportador: Mueve los vectores que forman el ángulo y anota los grados en cada caso. Veras que el eje de ROTACIÓN de los vectores es el punto A y te darás cuenta de que estas ROTANDO SEGMENTOS en UN PLANO
ACTIVIDAD 4: ¿En alguno de los casos anteriores ha cambiado la forma de la figura que has rotado?
Para determinar un giro o rotación es necesario conocer un punto, O, el centro de giro; un ángulo y el sentido de giro de ese ángulo. Existe el acuerdo de considerar positivo (+) al sentido contrario de las agujas de un reloj y sentido negativo (-) el de las agujas del reloj. Si A' es el punto girado de A, con centro O y ángulo a, entonces: /OA/ = /OA’/ y el segmento OA forma un ángulo a conel segmento OA’. Para girar una figura se giran TODOS los puntos que la forman. Esto hace que no se deforme.