Medianas, Baricentro y Áreas de Subtriángulos
Objetivo
Explorar cómo el baricentro de un triángulo (punto de intersección de sus medianas) lo divide en tres subtriángulos, observando si estos conservan áreas iguales al modificar la forma del triángulo.
Actividad 1: Construcción y exploración
Instrucciones:
- Observa las medianas construidas.
- Ubica el baricentro, el punto donde se cruzan las tres medianas.
- Mira las áreas de los subtriángulos generados.
- Mueve los vértices para cambiar la forma del triángulo.
- Verifica si las áreas cambian o se mantienen iguales.
Triángulo Equilátero: ¿Qué Revelan sus Medianeras?
Preguntas
¿Las áreas de los tres triángulos que se forman con el baricentro son iguales? ¿Por qué?
Cuando mueves los vértices del triángulo, ¿Cómo cambia la posición del baricentro? ¿Se mueve o se queda fijo? ¿Por qué?
Exploración en diferentes triángulos
Triángulo rectángulo
triangulo isósceles
Triángulo equilátero
Análisis Algebraico
Aquí veremos, paso a paso, cómo calcular el baricentro de un triángulo y demostrar algebraicamente que este punto lo divide en tres subtriángulos de igual área, sin importar la forma del triángulo.
Veamos un ejemplo de un triángulo equilátero con sus vértices ubicados en el plano cartesiano. Abajo están las coordenadas de los puntos y una imagen que muestra cómo queda el triángulo.
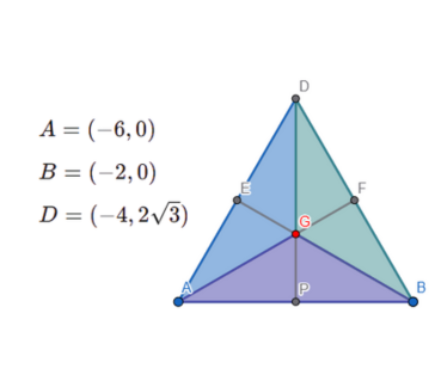
División en subtriángulos
El baricentro divide el triángulo original △ABC
- △AGB
- △DGB
- △ABG
¿Dónde está el centro del triángulo? Cálculo del baricentro paso a paso
En un triángulo, el baricentro es el punto donde se cruzan las tres medianas (líneas que van desde un vértice hasta el punto medio del lado opuesto)
¿Cómo se calcula?
Para encontrar el baricentro GGG, promediamos las coordenadas de los tres vértices del triángulo.
Si los vértices son:
Entonces, usamos la fórmula:
Sustituimos:
El baricentro del triángulo está en:
O, si prefieres un valor aproximado:
Entonces, usamos la fórmula:
Sustituimos:
El baricentro del triángulo está en:
O, si prefieres un valor aproximado:
¿Por qué es importante este punto?
El baricentro divide al triángulo en tres partes iguales en área y se comporta como el “centro de gravedad” del triángulo.
Área total del triángulo △ABD
Cuando tenemos un triángulo con vértices en coordenadas (x1,y1),(x2,y2),(x3,y3), podemos calcular su área utilizando la siguiente fórmula:
Esta fórmula nos permite calcular el área de cualquier triángulo a partir de las coordenadas de sus vértices sin necesidad de conocer la base ni la altura directamente.
Comprobación: Área del subtriángulo △ABG
Vamos a verificar cuánto mide el área del triángulo formado por los puntos A, B y el baricentro G.
Coordenadas:
Ahora calculamos el área del segundo subtriángulo formado por los puntos B, D y G.
Coordenadas:
Aplicamos la fórmula:
Comprobación: Área del subtriángulo △DAG
Por último, calculemos el área del tercer subtriángulo, formado por D, A y G
Coordenadas:
Esta fórmula nos permite calcular el área de cualquier triángulo a partir de las coordenadas de sus vértices sin necesidad de conocer la base ni la altura directamente.
Comprobación: Área del subtriángulo △ABG
Vamos a verificar cuánto mide el área del triángulo formado por los puntos A, B y el baricentro G.
Coordenadas:
Ahora calculamos el área del segundo subtriángulo formado por los puntos B, D y G.
Coordenadas:
Aplicamos la fórmula:
Comprobación: Área del subtriángulo △DAG
Por último, calculemos el área del tercer subtriángulo, formado por D, A y G
Coordenadas:
Conclusión final
Cada subtriángulo tiene área:
Responde las siguientes preguntas
¿Por qué crees que las áreas se reparten de forma equitativa?
conclusion
A través de este análisis, hemos comprobado que el baricentro de un triángulo divide la figura en tres subtriángulos de igual área.
Aunque el triángulo no sea equilátero, ni tenga lados iguales, el punto de intersección de sus medianas (el baricentro) siempre equilibra el área total de forma equitativa.