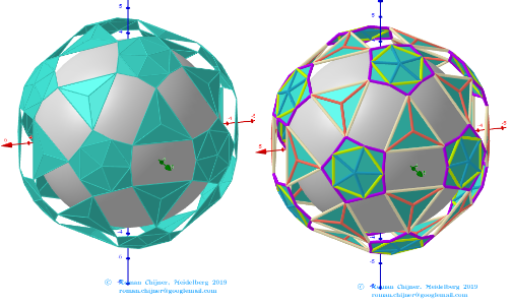
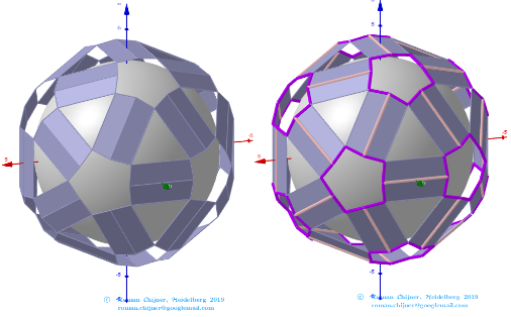
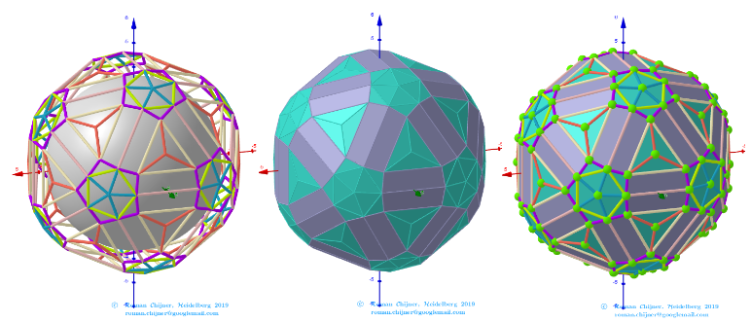
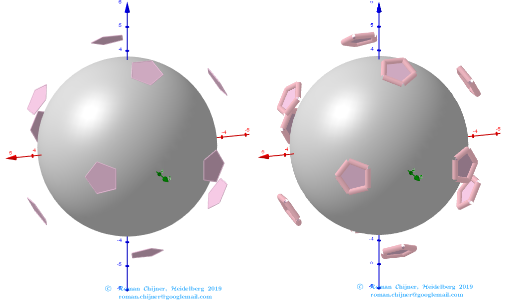
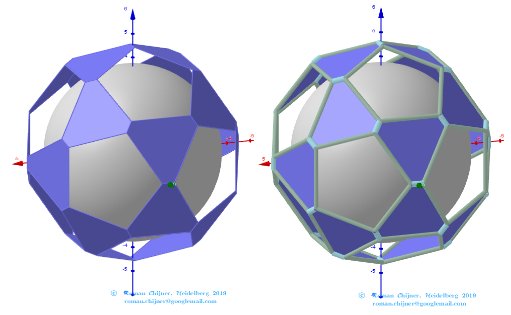
Images . Polyhedron(V=120) from Biscribed Pentakis Dodecahedron for the case of trisection of its 6th-order segments

The elements of the Biscribed Pentakis Dodecahedron(6).
Vertices: V = 120.
Faces: F =152. 120{3}+12{5}+20{6}.
Edges: E =270. 30+60+120+60- The order of the number of edges in this polyhedron according to their length.
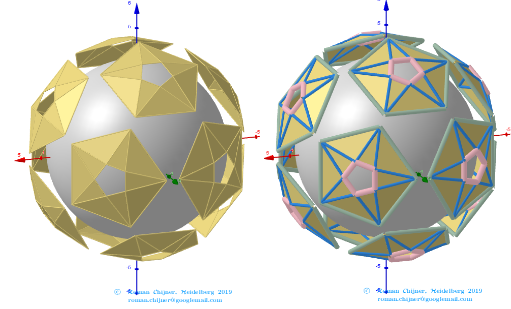
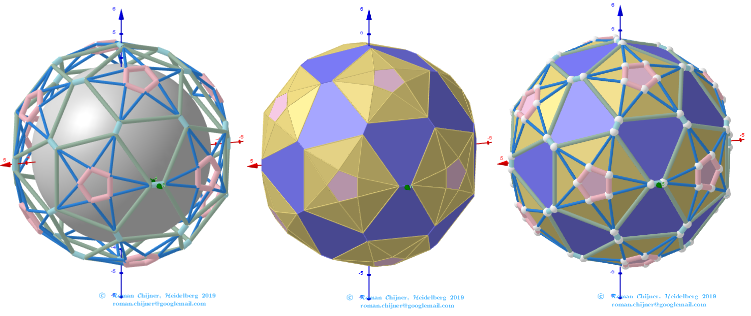
The elements of the dual to the Biscribed Pentakis Dodecahedron(6).
Vertices: V =152.
Faces: F =240. 180{3}+60{4}.
Edges: E =390. 120+60+60+60+60+30- The order of the number of edges in this polyhedron are according to their length.