Ángulos en polígonos
Contenido
- Concepto de polígono. Polígonos regulares y polígonos irregulares
- Suma de los ángulos interiores de un polígono
- Ángulos internos de polígonos regulares
Polígono
Polígono es una figura plana limitada por varios segmentos de recta.
Los polígonos se clasifican en irregulares y regulares.
Polígono regular es aquel que todos sus lados y todos sus ángulos interiores son congruentes.
Polígono irregular es aquel que no todos sus lados y no todos sus ángulos interiores son congruentes.
En la figura se muestran dos pentágonos (polígonos de 5 lados), el primero es regular mientras el segundo es irregular.
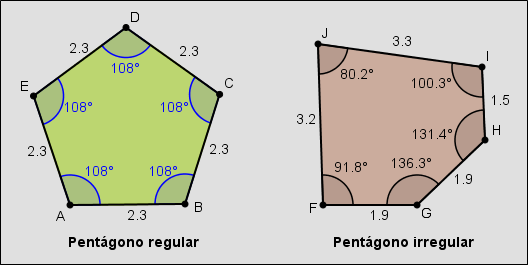
Suma de los ángulos interiores de un polígono
De la figura anterior se puede calcular la suma de los ángulos internos o interiores de cada uno de los dos polígonos:
La suma de los ángulos interiores de los dos pentágonos, sea regular o irregular, equivale a 540°.
En los dos applets siguientes se muestra un procedimiento para obtener la suma de los ángulos internos de un polígono.
La forma de los dos polígonos se puede modificar desplazando sus vértices.
El pentágono se descompone en tres triángulos que tienen en común el vértice A. La cantidad de triángulos equivale al número de lados disminuido en 2, es decir (n - 2).
Como se sabe que los ángulos de un triángulo suman 180°, entonces los ángulos del pentágono suman 180° x 3 = 540°.
El octágono del applet siguiente se descompone en 6 triángulos que tienen en común el vértice G. Como sucedió con el pentágono, la cantidad de triángulos equivale al número de lados disminuido en 2, es decir (n - 2).
Por lo tanto, la suma de los ángulos del octágono será 180° x 6 = 1080°.
De este análisis se puede concluir que la suma de los ángulos internos de un polígono está dada por la fórmula: suma = 180°(n - 2) donde n es el número de lados.
Si es un triángulo, n = 3:
Si es un cuadrado, n = 4:
Si es un octágono, n = 8:
Para descomponer el polígono se puede utilizar cualquiera de los vértices.
Ángulos internos de los polígonos regulares
Polígono regular es aquel que todos sus lados y todos sus ángulos interiores son congruentes.
Como ya se indicó, en un polígono cualquiera, la suma de los ángulos internos está dada por la fórmula
siendo n el número de lados del polígono.
Si el polígono es regular, todos los ángulos internos son congruentes. Por lo tanto, en todo polígono regular, la medida de cada ángulo interno está dada por la fórmula . Esto se muestra en los dos applets siguientes.
En un polígono regular se tiene los siguientes elementos fundamentales:
Lado: es cada uno de los segmentos que conforman el polígono
Circunferencia circunscrita: es la circunferencia que pasa por todos los vértices del polígono. Su centro es el centro del polígono.
Triángulo central: es cada uno de los triángulos formados por un lado y dos radios consecutivos de la circunferencia circunscrita. Ver el triángulo AOB
Cada triángulo central es isósceles porque tiene dos lados congruentes. Por lo tanto, el triángulo central tiene dos ángulos congruentes: ángulos OAB y ABO
Dado que un polígono regular tiene tantos triángulos centrales como lados tiene el polígono, la suma de los ángulos centrales equivale a 360°. De esa manera, la medida del ángulo central se puede calcular por la fórmula
Si el polígono es un octágono regular,
Del triángulo AOB se puede obtener la medida de :
En conclusión, el ángulo interno del octágono, . Este resultado es idéntico si se utiliza la fórmula con n = 8: